Aston 1922/Chapter 2: Difference between revisions

From Mass Spec Terms
← Older edit
No edit summary
 
(17 intermediate revisions by the same user not shown)
Line 1: Line 1:
<big><big>'''Chapter II - The Radioactive Isotopes'''</big></big>


==CHAPTER  II - THE  RADIOACTIVE  ISOTOPES==
{{Template:Aston 1922 Contents}}


==5. Chemical identities among the radioactive elements==
==5. Chemical identities among the radioactive elements==


Apart from the purely speculative considerations
Apart from the purely speculative considerations which have aheady been detailed, the theory of isotopes had its birth in the gigantic forward wave of human knowledge inaugurated by the discovery of radioactivity. It can admittedly be argued that, even if no radioactive elements existed, isotopes would inevitably have been discovered by the method of positive rays. But progress must then have been exceedingly slow, and the arrival at the real interpretation of the idea, depending as it does on Sir [[wikipedia:Ernest Rutherford|Ernest Rutherford]]'s theory of the " nucleus" atom, almost impossible.
which have aheady been detailed, the theory of isotopes had
its birth in the gigantic forward wave of human knowledge
inaugurated by the discovery of radioactivity. It can admit-
tedly be argued that, even if no radioactive elements existed,
isotopes would inevitably have been discovered by the method
of positive rays. But progress must then have been exceed-
ingly slow, and the arrival at the real interpretation of the idea,
depending as it does on Sir [[wikipedia:Ernest Rutherford|Ernest Rutherford]]'s theory of
the " nucleus" atom, almost impossible.


In 1906 [[wikipedia:Bertram Boltwood|Boltwood]] at Yale discovered a new element in the
In 1906 [[wikipedia:Bertram Boltwood|Boltwood]] at Yale discovered a new element in the radioactive group which he called [[wiktionary:ionium|Ionium]],<ref>Boltwood, ''Amer. J. Sci'', '''22''', 537, 1906;[https://www.proquest.com/docview/89598254?pq-origsite=gscholar&fromopenview=true&sourcetype=Scholarly%20Journals] '''24''', 370, 1907.[https://www.proquest.com/docview/89598004/fulltextPDF/1D7013FDBDF94219PQ/1?accountid=12154&sourcetype=Scholarly%20Journals]</ref> and described as having chemical properties similar to those of thorium. So much was this the case that if, by accident, salts of these two elements were mixed, he found it impossible to separate them again by any of the chemical processes.
radioactive group which he called [[wiktionary:ionium|Ionium]],<ref>Boltwood, ''Amer. J. Sci'', '''22''', 537, 1906;[https://www.proquest.com/docview/89598254?pq-origsite=gscholar&fromopenview=true&sourcetype=Scholarly%20Journals] '''24''', 370, 1907.[https://www.proquest.com/docview/89598004/fulltextPDF/1D7013FDBDF94219PQ/1?accountid=12154&sourcetype=Scholarly%20Journals]</ref> and described
as having chemical properties similar to those of thorium.
So much was this the case that if, by accident, salts of these
two elements were mixed, he found it impossible to separate
them again by any of the chemical processes.


Boltwood, being occupied in the experimental proof that
Boltwood, being occupied in the experimental proof that ionium was the parent substance of radium, did not pursue this line of investigation further at the time, but the work was later taken in hand by Marckwald and Keetman of Berlin.<ref>Keetman, ''Jahr. Radioactivitat'', '''6''', 269, 1909.</ref> Thanks to the rapid advance in radioactive methods there were now at command means of detecting change in concentration of a delicacy unheard of in the previous work on the rare earths, but yet, after years of patient and laborious work, not the slightest sign of separation of ionium and thorium could be observed. The chemical similarity between these two bodies was therefore of an order entirely different to that exhibited by the rare earth elements, and came as near absolute identity as the most critical mind could require.
ionium was the parent substance of radium, did not pursue
this line of investigation further at the time, but the work
was later taken in hand by Marckwald and Keetman of Berlin.<ref>Keetman, ''Jahr. Radioactivitat'', '''6''', 269, 1909.</ref> Thanks to the rapid advance in radioactive methods there
were now at command means of detecting change in concentration of a delicacy unheard of in the previous work on the
rare earths, but yet, after years of patient and laborious work,
not the slightest sign of separation of ionium and thorium
could be observed. The chemical similarity between these
two bodies was therefore of an order entirely different to that
exhibited by the rare earth elements, and came as near absolute
identity as the most critical mind could require.


This result was confirmed in the most rigorous manner by
This result was confirmed in the most rigorous manner by [[wikipedia:Carl Auer von Welsbach|Auer v. Welsbach]]<ref>A. von Welsbach, ''Wien. Ber.'' iia, 119, 1011, 1910.</ref> who was able to apply to the problem his valuable experience in work on the rare earths.
[[wikipedia:Carl Auer von Welsbach|Auer v. Welsbach]]<ref>A. von Welsbach, ''Wien. Ber.'' iia, 119, 1011,   1910.</ref> who was able to apply to the problem
his valuable experience in work on the rare earths.


Furthermore, [[wiktionary:mesothorium|Mesothorium]], discovered by Hahn in 1907,
Furthermore, [[wiktionary:mesothorium|Mesothorium]], discovered by Hahn in 1907, was shown to be chemically inseparable from radium by Marckwald<ref>Marckwald, ''Ber. d. Chem. Oes.'', '''40''', 3420, 1910.</ref> and Soddy<ref>Soddy, ''Trans. Chem. Soc'', '''99''', 72, 1911.</ref> and similar chemical identities were shown to be exceedingly probable in many other cases of radioactive products. Certain regularities in the occurrence of these were pointed out by [[wikipedia:Otto Hahn|Hahn]] and [[wikipedia:Lise Meitner|Meitner]].<ref>Hahn and Meitner, ''Physikal. Zeitsch.'', '''11''', 493, 1910.</ref>
was shown to be chemically inseparable from radium by
Marckwald<ref>Marckwald, ''Ber. d. Chem. Oes.'', '''40''', 3420, 1910.</ref> and Soddy<ref>Soddy, ''Trans. Chem. Soc'', '''99''', 72, 1911.</ref> and similar chemical identities were
shown to be exceedingly probable in many other cases of
radioactive products. Certain regularities in the occurrence
of these were pointed out by [[wikipedia:Otto Hahn|Hahn]] and [[wikipedia:Lise Meitner|Meitner]].<ref>Hahn and Meitner, ''Physikal. Zeitsch.'', '''11''', 493, 1910.</ref>


The situation was admirably summed up by Soddy in his
The situation was admirably summed up by Soddy in his report on radioactivity for the year 1910<ref>Soddy, ''Chem. Soc. Ann. Rep.'', '''285''', 1910.</ref> in the following words:
report on radioactivity for the year 1910<ref>Soddy, ''Chem. Soc. Ann. Rep.'', '''285''', 1910.</ref> in the following words:  


"These regularities may prove to be the beginning of some
<blockquote>"These regularities may prove to be the beginning of some embracing generalisation, which will throw light, not only on radioactive processes, but on elements in general and the Periodic Law. Of course, the evidence of chemical identity is not of equal weight for all the preceding cases, but the complete identity of ionium, thorium and radiothorium, of radium and mesothorium 1, of lead and radium D, may be considered thoroughly established. . . . The recognition that elements of different atomic weights may possess identical properties seems destined to have its most important apphcation in the region of inactive elements, where the absence of a second radioactive nature makes it impossible for chemical identity to be individually detected. Chemical homogeneity is no longer a guarantee that any supposed element is not a mixture of several of different atomic weights, or that any atomic weight is not merely a mean number. The constancy of atomic weight, whatever the source of the material, is not a complete proof of homogeneity, for, as in the radioelements, genetic relationships might have resulted in an initial constancy of proportion between the several individuals, which no subsequent natural or artificial chemical process would be able to disturb. If this is the case, the absence of simple numerical relationships between the atomic weights becomes a matter of course rather than one of surprise."</blockquote>
embracing generalisation, which will throw light, not only on
radioactive processes, but on elements in general and the
Periodic Law. Of course, the evidence of chemical identity
is not of equal weight for all the preceding cases, but the
complete identity of ionium, thorium and radiothorium, of
radium and mesothorium 1, of lead and radium D, may be
considered thoroughly established. . . . The recognition
that elements of different atomic weights may possess identical
properties seems destined to have its most important apphca-
tion in the region of inactive elements, where the absence of
a second radioactive nature makes it impossible for chemical
identity to be individually detected. Chemical homogeneity
is no longer a guarantee that any supposed element is not a
mixture of several of different atomic weights, or that any
atomic weight is not merely a mean number. The constancy
of atomic weight, whatever the source of the material, is not
a complete proof of homogeneity, for, as in the radioelements,
genetic relationships might have resulted in an initial constancy
of proportion between the several individuals, which no subsequent natural or artificial chemical process would be able to
disturb. If this is the case, the absence of simple numerical
relationships between the atomic weights becomes a matter of
course rather than one of surprise."


===6. Spectroscopic identity of isotopes=== 
==6. Spectroscopic identity of isotopes==
The  next  great
advance  was  of  an  even  more  revolutionary  character.  This
consisted  in  the  demonstration  that  the  chemically  indistin-
guishable products  of  the  transformation  of  the  radioactive
elements  might  also  be  spectroscopically  identical.  The  idea
that  elements  of  different  atomic  weight  might  yet  have  the
same  spectrum  originated  in  Sir  Ernest  Rutherford's  laboratory
and  appears  to  have  been  first  entertained  by  A.  S.  Russell.
With  Rossi  ^  he  undertook  the  comparison  between  the  spec-
trum of  pure  thorium  and  that  of  a  mixture  of  thorium  and
ionium  which  radioactive  evidence  showed  to  contain  a  large
percentage  of  the  latter  element.  No  new  fines  attributable
to  ionium  were  observed  ;  in  fact  the  spectra  obtained  were
absolutely    indistinguishable.


After  giving  in full  the radioactive evidence as  to the  probable=
The next great advance was of an even more revolutionary character. This consisted in the demonstration that the chemically indistinguishable products of the transformation of the radioactive elements might also be spectroscopically identical. The idea that elements of different atomic weight might yet have the same spectrum originated in Sir Ernest Rutherford's laboratory and appears to have been first entertained by [https://www.nature.com/articles/237120a0.pdf A. S. Russell]. With Rossi<ref>Russell and Rossi, ''Proc. Roy. Soc'', '''77A''', 478, 1912.</ref> he undertook the comparison between the spectrum of pure thorium and that of a mixture of thorium and ionium which radioactive evidence showed to contain a large percentage of the latter element. No new fines attributable to ionium were observed; in fact the spectra obtained were absolutely indistinguishable.


percentage of ionium present, and showing that it was prac-
After giving in full the radioactive evidence as to the probable percentage of ionium present, and showing that it was practically impossible for this to be too small for its spectrum to appear, the writers go on as follows:
tically impossible for this to be too small for its spectrum to=


appear, the writers  go  on  as  foUows  :  
<blockquote>"There are, however, two other possible ways of explaining our failure to obtain a distinct spectrum for ionium, besides the one discussed above.  It is possible that :


" There  are,  however,  two  other  possible  ways  of  explaining
"(1) Ionium has no arc spectrum in the region investigated,
our  failure  to  obtain  a  distinct  spectrum for  ionium, besides  the=


one  discussed  above.    It  is  possible  that :
"  (1)  Ionium  has  no  arc  spectrum  in  the  region  investigated,
or
or


" (2) Ionium and thorium have identical spectra in the region
"(2) Ionium and thorium have identical spectra in the region investigated.
investigated.
 
"  The  first  possibifity  is  highly  improbable,  for  all  solids  of=
 
high  atomic  weights  have  arc  spectra,  and,  further,  aU  rare
earths  have  highly  comphcated  spectra.
 
"  The  second  possibifity,  though  somewhat  speculative
in  nature,  is  suggested  by  some  recent  work  on  the  chemical
properties  of  the  radio-elements.  There  is  no  evidence
at  present  to  disprove  its  truth.  It  is  well  known  that  there
are  no  less  than  four  sets  of  longfived  radio-elements,  the
 
1  Russell  and  Rossi,  Proc.  Roy.  Soc,  77A,  478,    1912.
 
 
10  ISOTOPES
 
members  of  each  of  which  are  chemically  non-separable.  These
elements  do  not  all  belong  to  the  group  of  rare  earths,  many
non-radioactive  members  of  which  are  known  to  be  chemically
very  similar.  Mesothorium,  for  instance,  which  is  chemically
non-separable '  from  radium,  belongs  to  the  alkahne  earth
group.  Again  the  two  non-separable  a  ray  products  which
are  present  in  ordinary  uranium,  and  which  have  been  called
by  Geiger  and  Nuttall  uranium  I  and  uranium  II  belong  to
the  chromium-molybdenum-tungsten  group  of  elements.  The
explanation  of  these  striking  chemical  similarities  is  very
probably  that  the  two  very  similar  bodies  are  really  different
members  of  the  same  group  of  elements,  the  difference  in  their
chemical  properties  being  less  pronounced  than  the  difference
between  other  members  of  the  same  group,  owing  to  the  small
difference  in  their  atomic  weights.  But  the  possibility  that
they  are  identical  in  all  physical  and  chemical  properties,  and
differ  only  in  atomic  weight  and  in  radioactive  properties,  should=
 
not  be  lost  sight  of.  If  this  explanation  should  eventually  prove=
 
justified,  the  spectrum  of  ionium  would  he  identical  with  that  of=
 
thorium."
 
It  is  not  surprising  that  the  idea  was  put  forward  with  some
caution.  Unhke  that  of  chemical  identity  which  had  been
led  up  to  by  a  gradual  series  of  steps,  it  was  entirely  new  an=
d
contrary  to  all  the  preconceived  ideas  of  the  relations  between
the  spectrum  of  an  element  and  the  masses  of  its  atoms.  The
new  departure  was  supported  by  Soddy  ^  but  received  some
adverse  criticism  on  the  ground  of  insufficient  evidence.  The
later  work  bearing  on  this  point  will  be  described  in  Chapter  X.=
 
 
Ah-eady  in  1911  the  theory  of  the  "  Nucleus  Atom  "  2  had
been  formulated.  This  gave  the  first  hint  as  to  the  physical
meaning  of  chemical  and  spectroscopic  identity,  namely  that
the  nuclei  of  atoms  might  vary  in  their  mass  but  yet,  at  the
same  time,  possess  some  property  in  common  with  each  other,
namely  nuclear  charge,  upon  which  the  chemistry  and  spectra
depend.
 
In  1912  appeared  the  electrochemical  work  of    Hevesy,*
 
1  Soddy,  Chem.  News,  Feb.  28,  1913.  *  F.  p.  92.
 
3  G.  Hevesy,  Phil.  Mag.,  23,  628,  1912  ;  Physikal.  Zeitsch.  15, =
672,
715,    1912.
 
 
THE  RADIOACTIVE  ISOTOPES  11
 
which  led  to  the  discovery  of  the  remarkable  field  of  research
opened  up  by  the  use  of  radioactive  bodies  as  indicators.^  A
Httle  later  Paneth  and  Hevesy  were  able  to  show  the  complete
identity  of  the  electrochemical  properties  of  Radium  D  and
Lead.2
 
In  1914  Rutherford  and  Andrade  ^  examined  the  self -excited
X-ray  spectrum  of  radium  B.  They  used  a  crystal  of  rock
salt  for  the  analysis  and  got  rid  of  the  effect  of  the  swift  ^=
 
rays  by  putting  the  source  in  a  strong  magnetic  field.  The  wave=
 
length  of  the  L  radiation  proved  to  be  exactly  that  expected
for  lead  from  Moseley's  experiment.*  This  was  the  first
proof  that  isotopes  had  identical  X-ray  spectra.  The  actual
values  for  ordinary  lead  were  subsequently  determined  by
Siegbahn  and  found  to  be  in  excellent  agreement  with  Ruther-
ford and  Andrade's  results.
 
===7.  The  Chemical  Law  of  Radioactive  change===
This
law,  put  in  the  briefest  form,  asserts  :  A  radioactive  element
when  it  loses  an  alpha  particle  goes  back  two  places  in  the
Periodic  Table  ;  when  it  loses  a  beta  particle  it  goes  forward=
 
one  place.
 
The  law  has  been  associated  with  the  name  of  Soddy  ^  who
was  the  first  to  suggest,  in  the  form  of  a  valency  property,
that  part  of  it  relating  to  alpha  rays.^  But  in  its  more  com-=
 
plete enunciation,  which  took  place  early  in  1913,  at  least
four  other  investigators  can  claim  a  share.
 
RusseU  was  the  first  to  pubhsh  a  law  covering  both  Idnds  of
rays,'  but  owing  to  the  fact  that  he  failed  to  reaHse  that  the=
 
sequence  of  elements  in  the  periodic  table  is  a  continuous  ex-
pression, his  statement  was  not  so  simple  and  definite  as  it  migh=
t
have  been.    Fajans,^  using  as  foundation  the  electrochemical
 
^  F.  p.  19.
 
2  Paneth  and  Hevesy,  Sitzungber.  K.  Akad.  Wiss.  Wien,  iiA,  123,=
 
1037,    1913.
 
3  Rutherford  and  Andrade,  Phil.  Mag.  27,  854,  1914.      *  V.  p.=
  93.
 
^  V.  Stewart,  Recent  Advances  in  Physical  and  Inorganic  Chemistry,=
 
Longmans,  1919.
 
^  Soddy,  The  Chemistry  of  the  Radio  Elements,  29,  First  Edition,=
 
Longmans,    1911.
 
'  Russell,  Chem.  News,  Jan,  31,  1913,
 
8  Fajans,  Physikal.  Zeitsch.  Feb.  15,  1913.
 
 
12  ISOTOPES
 
results  of  Hevesy,^  and  Soddy,  working  on  the  results  of  a
very  full  chemical  investigation  carried  out  at  his  request  by
Fleck,  2  pubUshed  the  generalisation  in  its  full  and  complete
form  independently,  and  practically  at  the  same  time.
 
This  law,  which  will  be  shown  later  to  be  a  natural  conse-
quence of  the  much  wider  generahsation  discovered  by  Moseley,^
has  been  of  the  greatest  value  in  correlating  the  numerous
products  of  radioactive  change,  and  predicting  with  accuracy
which  of  them  mil  have  identical  properties.  To  the  latter
the  name  Isotopes  was  apphed  by  Soddy  in  the  following
words :  "  The  same  algebraic  sum  of  the  positive  and
negative  charges  in  the  nucleus  when  the  arithmetical  sum
is  different  gives  what  I  call  '  isotopes  '  or  '  isotopic  eleme=
nts  '
because  they  occupy  the  same  place  in  the  periodic  table.
They  are  chemically  identical,  and  save  only  as  regards  the
relatively  few  physical  properties  which  depend  upon  atomic
mass  directly,  physically  identical  also."  Any  element  which
is  the  result  of  a  series  of  changes  involving  the  loss  of  twic=
e
as  many  beta  particles  as  alpha  particles  must  clearly  be  the
isotope  of  the  parent  element,  since  it  must  inevitably,  by  the=
 
above  law,  reach  the  same  place  in  the  periodic  table  at  the  en=
d
of  these  operations.
 
===8.  Isobares=== 
Just  as  we  can  have  elements  of  the  same
chemical  properties  but  different  atomic  weight  so  we  can  also
have  those  with  the  same  atomic  weight  but  different  chemical
properties.  These  Stewart  *  has  called  "  Isobares."  Any
product  due  to  the  loss  of  a  beta  ray  (which  has  a  negligible=
 
mass)  5  must  be  an  isobare  of  its  parent  substance,  for,  without=
 
change  of  mass,  it  has  moved  in  the  periodic  table  and  so
changed  its  chemical  properties.  It  is  interesting  to  note  in
this  connection  that  no  isobare  has  actually  been  discovered
among  the  non-radioactive  elements  as  yet,  but  they  must
certainly  exist.*'
 
^  Hevesy,  Physihal.  Zeitsch.  Jan.  15,  1913.
 
2  Fleck,  Trans.  Chem.  Soc.  103,  381,  1052,    1913.
 
3  V.  p.  93.
 
*  Stewart,  Phil.  Mag.  36,  326,    1918.
'  V.  p.  91.
  V.  p.  77.
 
 
THE  RADIOACTIVE  ISOTOPES  13
 
===9.  The  Radioactive  Transformations=== 
The  radioactive
elements  are  all  formed  from  the  two  parent  elements  inanium
and  thorium  by  a  series  of  changes  or  transformations.  These
changes  can  be  classified  according  to  their  nature  into  two
types.  In  the  first  type  of  change  called  the  a  ray  change
the  atom  loses  a  particle  of  mass  4  carrying  two  positive
charges  {+  2e)  which  has  been  identified  with  the  nucleus
of  the  helium  atom.^  In  the  second  or  ^  ray  change  the
particle  shot  off  has  a  neghgible  mass  and  carries  a  single
negative  charge  (  e).  Hence  in  an  a  ray  change  the  ele=
-
ment loses  4  units  in  atomic  weight,  while  in  a  /3  ray  change
its  weight  is  unaltered.
 
The  rate  of  decay  of  an  element  is  measured  by  the  "  half
value  "  period  which  may  vary  from  10^=C2=B0  years  to  10 ~^^  of =
a
second.  The  velocity  with  which  the  rays  are  ejected  also
varies  and  is  apparently  connected  with  the  period  of  the
element  by  the  very  interesting  relation  of  Geiger  and  NuttaU.^
The  intricate  researches  by  which  the  complex  series  of  trans-
formations have  been  explained  belong  to  the  subject  of
Radioactivity  and  cannot  be  described  here.  From  the  point
of  view  of  isotopes  it  will  be  enough  to  consider  the  final
results  which  are  given  in  the  two  diagrams  (Figs.  1  and  2).
 
In  the  first  of  these,  which  is  due  to  Soddy,^  the  nuclear
charge  or  Atomic  number,'*  upon  which  all  the  chemical
and  spectroscopic  properties  of  the  elements  depend,  and
which  expresses  its  position  in  the  periodic  table,  is  indicated=
 
by  a  series  of  columns  edged  with  thick  fines  sloping  down-
wards to  the  right.  The  atomic  weights  are  shown  by  fine
lines  sloping  in  the  opposite  direction.  The  fines  corre-
sponding to  even  atomic  weights  have  been  omitted  to  simpfify
the  scheme.  AU  elements  lying  in  the  same  column  will
therefore  be  isotopes  and  all  elements  lying  on  the  same  fine
sloping  up  to  the  right  will  be  isobares.  The  a  and  ^  ray
changes  are  shown  by  arrows  and  the  period  of  decay  of  the
elements  indicated  by  times  expressed  in  suitable  units.
 
1  V.  Table  p.  106.
 
*  Rutherford,  Radioactive  Substances  and  their  Radiations,  p.  607,=
 
Cambridge,  1913.
 
3  Soddy,  Trans.  Chem.  Soc,  U5,  16,    1919.  *  V.  p.  93.
 
 
14
 
 
ISOTOPES
 
 
Fig.  1.  Diagram  of  the  transformations  of  the  radio-elemen=
ts  showing
atomic  number,  atomic  weight  and  period  of  disintegration  of  each=
 
product.
 
 
THE  RADIOACTIVE  ISOTOPES
 
 
16
 
 
The  second  diagram  ^  is  arranged  in  a  simple  manner  to
show  the  general  chains  of  transformation  at  a  glance.  In  it
the  a  and  /5  ray  changes  are  plotted  against  atomic  number
and  the  other  information  omitted.  On  this  diagram  all
elements  lying  on  the  same  horizontal  level  will  be  isotopes.
To  take  an  example,  uranium  I  which  has  an  atomic  number
92  and  an  atomic  weight  238  loses  one  a  particle  and  becomes
uranium  X,  atomic  number  90,  atomic  weight  234,  This  then
gives  off  two  /3  rays  in  succession,  first  becoming  uranium  X2
 
 
Uranium    U.ji
 
 
Profoachnium
 
 
U.x,    Ionium      U.Y    \    Rac/ioact.      Thorium  Radioth.
j  Actinium  Mikj^
 
 
Racfu
 
 
Ra.  Emanation
 
 
Polonium        RaC        Ra.A  AcC^
 
Ral/      R^.C
 
 
AcX  Mesoth.j    Th'.X
 
 
A  C.Em.
 
 
Tti.Em.
 
 
Ac.  A
 
 
Ra.D  Pb
\
Ra.
 
 
\
 
 
Ra.B      Pb    Pb.
 
 
AcC
\
 
 
\
 
 
n.Ci
/  \
 
 
TfiA
 
 
Ac.D
 
 
Ac.B      P6.    P6.
 
 
ThC


"The first possibility is highly improbable, for all solids of high atomic weights have arc spectra, and, further, aU rare earths have highly complicated spectra.


Tfy.B
"The second possibility, though somewhat speculative in nature, is suggested by some recent work on the chemical properties of the radio-elements. There is no evidence at present to disprove its truth. It is well known that there are no less than four sets of longlived radio-elements, the members of each of which are chemically non-separable. These elements do not all belong to the group of rare earths, many non-radioactive members of which are known to be chemically very similar. Mesothorium, for instance, which is chemically non-separable ' from radium, belongs to the alkaline earth group. Again the two non-separable a ray products which are present in ordinary uranium, and which have been called by Geiger and Nuttall uranium I and uranium II belong to the chromium-molybdenum-tungsten group of elements. The explanation of these striking chemical similarities is very probably that the two very similar bodies are really different members of the same group of elements, the difference in their chemical properties being less pronounced than the difference between other members of the same group, owing to the small difference in their atomic weights. But the possibility that they are identical in all physical and chemical properties, and differ only in atomic weight and in radioactive properties, should not be lost sight of. If this explanation should eventually prove justified, the spectrum of ionium would he identical with that of thorium."</blockquote>


It is not surprising that the idea was put forward with some caution. Unlike that of chemical identity which had been led up to by a gradual series of steps, it was entirely new and contrary to all the preconceived ideas of the relations between the spectrum of an element and the masses of its atoms. The new departure was supported by Soddy<ref>Soddy, ''Chem. News'', Feb. 28, 1913.</ref> but received some adverse criticism on the ground of insufficient evidence. The later work bearing on this point will be described in Chapter X.


Th.D
Already in 1911 the theory of the "Nucleus Atom"<ref>V. p. 92.</ref> had been formulated. This gave the first hint as to the physical meaning of chemical and spectroscopic identity, namely that the nuclei of atoms might vary in their mass but yet, at the same time, possess some property in common with each other, namely nuclear charge, upon which the chemistry and spectra depend.


In 1912 appeared the electrochemical work of  [[wikipedia:George de Hevesy|Hevesy]],<ref>G. Hevesy, ''Phil. Mag.'', 23, 628, 1912 ; ''Physikal. Zeitsch.'' '''15''', 672, 715, 1912.</ref> which led to the discovery of the remarkable field of research opened up by the use of radioactive bodies as indicators.<ref>V. p. 19.</ref> A little later [[wikipedia:Friedrich Paneth|Paneth]] and Hevesy were able to show the complete identity of the electrochemical properties of [[wikipedia:Isotopes of lead|Radium D]] and Lead.<ref>Paneth and Hevesy, Sitzungber. K. Akad. Wiss. Wien, iiA, 123, 1037,  1913. </ref>


92
In 1914 Rutherford and [[wikipedia:Edward Andrade|Andrade]]<ref>Rutherford and Andrade, Phil. Mag. 27, 854, 1914.    </ref> examined the self-excited X-ray spectrum of [[wikipedia:Polonium-210|radium B]]. They used a crystal of rock salt for the analysis and got rid of the effect of the swift &#946; rays by putting the source in a strong magnetic field. The wave length of the L radiation proved to be exactly that expected for lead from Moseley's experiment.<ref>V. p. 93. </ref> This was the first proof that isotopes had identical X-ray spectra. The actual values for ordinary lead were subsequently determined by [[wikipedia:Manne Siegbahn|Siegbahn and found to be in excellent agreement with Rutherford and Andrade's results.


91
==7. The Chemical Law of Radioactive change==


90
This law, put in the briefest form, asserts: A radioactive element when it loses an alpha particle goes back two places in the Periodic Table; when it loses a beta particle it goes forward one place.


89
The law has been associated with the name of Soddy<ref>V. Stewart, ''Recent Advances in Physical and Inorganic Chemistry'', Longmans, 1919.</ref>  who was the first to suggest, in the form of a valency property, that part of it relating to alpha rays.<ref>Soddy, ''The Chemistry of the Radio Elements'', 29, First Edition, Longmans,  1911. </ref> But in its more complete enunciation, which took place early in 1913, at least four other investigators can claim a share.


^Z
Russell was the first to publish a law covering both Kinds of rays,<ref>Russell, ''Chem. News,'' Jan, 31, 1913, </ref> but owing to the fact that he failed to realise that the sequence of elements in the periodic table is a continuous expression, his statement was not so simple and definite as it might have been. [[wikipedia:Kazimierz Fajans|Fajans]],<ref>Fajans, ''Physikal. Zeitsch.'' Feb.  15, 1913. </ref> using as foundation the electrochemical results of [[wikipedia:George de Hevesy|Hevesy]],<ref>Hevesy, ''Physikal. Zeitsch.'' Jan.  15,  1913. </ref> and Soddy, working on the results of a very full chemical investigation carried out at his request by Fleck,<ref>Fleck, Trans. Chem. Soc. 103, 381,  1052,  1913. </ref> published the generalisation in its full and complete form independently, and practically at the same time.


87
This law, which will be shown later to be a natural consequence of the much wider generalisation discovered by Moseley,<ref>V. p. 93. </ref> has been of the greatest value in correlating the numerous products of radioactive change, and predicting with accuracy which of them mil have identical properties. To the latter the name Isotopes was appled by Soddy in the following words: "The same algebraic sum of the positive and negative charges in the nucleus when the arithmetical sum is different gives what I call 'isotopes' or 'isotopic elements' because they occupy the same place in the periodic table. They are chemically identical, and save only as regards the relatively few physical properties which depend upon atomic mass directly, physically identical also." Any element which is the result of a series of changes involving the loss of twice as many beta particles as alpha particles must clearly be the isotope of the parent element, since it must inevitably, by the above law, reach the same place in the periodic table at the end of these operations.


86
==8. Isobares==


85
Just as we can have elements of the same chemical properties but different atomic weight so we can also have those with the same atomic weight but different chemical properties. These [[wikipedia:Alfred Walter Stewart|Stewart]] <ref>Stewart, ''Phil. Mag.'' '''36''', 326, 1918.[{{doi}}10.1080/14786441008635836] </ref> has called "[[Isobar]]es." Any product due to the loss of a [[wikipedia:Beta particle|beta ray]] (which has a negligible mass)<ref>V. p. 91. </ref> must be an isobare of its parent substance, for, without change of mass, it has moved in the periodic table and so changed its chemical properties. It is interesting to note in this connection that no isobare has actually been discovered among the non-radioactive elements as yet, but they must certainly exist.<ref>V. p. 77. </ref>


84
==9. The Radioactive Transformations==


83
[[File:Aston 1922 Figure 1.jpg|thumb|400 px|Fig. 1. Diagram of the transformations of the radio-elements showing atomic number, atomic weight and period of disintegration of each product.]] The radioactive elements are all formed from the two parent elements inanium and thorium by a series of changes or transformations. These changes can be classified according to their nature into two types. In the first type of change called the &alpha; ray change the atom loses a particle of mass 4 carrying two positive charges {+2''e'') which has been identified with the nucleus of the helium atom.^<ref>V. Table p. 106. </ref> In the second or &beta; ray change the particle shot off has a negligible mass and carries a single negative charge (–e). Hence in an a ray change the element loses 4 units in atomic weight, while in a &beta; ray change its weight is unaltered.


82
The rate of decay of an element is measured by the " half value " period which may vary from 10<sup>10</sup> years to 10<sup>-11</sup> of  a second. The velocity with which the rays are ejected also varies and is apparently connected with the period of the element by the very interesting relation of [[wikipedia:Geiger–Nuttall law|Geiger and Nuttall.<ref>Rutherford, Radioactive Substances and their Radiations, p. 607, Cambridge, 1913. </ref> The intricate researches by which the complex series of transformations have been explained belong to the subject of Radioactivity and cannot be described here. From the point of view of isotopes it will be enough to consider the final results which are given in the two diagrams (Figs. 1 and 2).


81
In the first of these, which is due to Soddy,<ref>Soddy, Trans. Chem. Soc, U5, 16,  1919.</ref> the nuclear charge or Atomic number,<ref>V. p. 93.  </ref> upon which all the chemical and spectroscopic properties of the elements depend, and which expresses its position in the periodic table, is indicated by a series of columns edged with thick fines sloping downwards to the right. The atomic weights are shown by fine lines sloping in the opposite direction. The fines corresponding to even atomic weights have been omitted to simplify the scheme. All elements lying in the same column will therefore be ''isotopes'' and all elements lying on the same fine sloping up to the right will be ''isobares''. The &alpha; and &beta; ray changes are shown by arrows and the period of decay of the elements indicated by times expressed in suitable units.


[[File:Aston 1922 Figure 2.jpg|thumb|600 px|Fig. 2. Diagram of the radioactive transformations in relation to atomic
[[File:Aston 1922 Figure 2.jpg|thumb|400 px|left|Fig. 2. Diagram of the radioactive transformations in relation to atomic numbers. In every case a step two downwards is accompanied by the emission of an a particle and one downwards by a &beta; particle.]]
numbers. In every case a step two downwards is accompanied by the
emission of an a particle and one downwards by a &beta; particle.]]


and then Uranium II. Uranium II has an atomic number
The second diagram<ref>Darwin, ''Nature'', '''106''', 82, 1920.[https://archive.org/details/naturejournal106londuoft/page/82/mode/1up]</ref>  is arranged in a simple manner to show the general chains of transformation at a glance. In it the &alpha; and &beta;ray changes are plotted against atomic number and the other information omitted. On this diagram all elements lying on the same horizontal level will be isotopes. To take an example, uranium I which has an atomic number 92 and an atomic weight 238 loses one &alpha; particle and becomes [[wikipedia:Protactinium|uranium X]], atomic number 90, atomic weight 234, This then gives off two &beta; rays in succession, first becoming [[wikipedia:Isotopes of protactinium|uranium X2]] and then [[wikipedia:Isotopes of uranium|Uranium II]]. Uranium II has an atomic number 92 so that it is an isotope of uranium I. It has an atomic weight 234 so it is anisobare of uranium Xi and uranium X2. Uranium II can disintegrate by shooting off an a particle in two different ways ; about 8 per cent, of its atoms appear to form uranium Y, which is probably the parent substance of the actinium series. Disregarding this for the moment and following the main chain, 92 per cent, of the atoms of uranium II suffer an &alpha; ray change and are transformed into ionium, atomic weight 230, atomic number 90. Ionium loses an a particle and becomes radium, atomic weight 226. This by the same process changes to radium emanation, then to radium A, and then to radium B with atomic weight 214, We see that uranium II has lost 5 &alpha; particles in succession, thereby coming back 10 places, 92-82 in the periodic table, and its atomic weight has been reduced 20 units in the process. Radium B loses a &beta; particle, becoming radium C which can disintegrate in two different ways. An extremely small proportion, 0.03 per cent., of its atoms undergo an &alpha; ray change to radium C2 which then loses a &beta; particle and may become inactive lead of atomic weight 210. The vast majority of the atoms of radium C lose a &beta; particle and form radium C. This next loses an a particle and becomes radium D, an active isotope of lead of atomic weight 210. Radium D now loses two &beta; particles in succession, becoming radium E and then radium E, which is also called [[wikipedia:polonium|polonium]]. This finally undergoes its last a ray change and becomes inactive uranium lead of atomic weight 206.
92 so that it is an isotope of uranium I. It has an atomic
weight 234 so it is anisobare of uranium Xi and uranium X2.
Uranium II can disintegrate by shooting off an a particle in
two different ways ; about 8  per cent, of its atoms  appear to=


form  uranium  Y, which  is  probably  the parent substance  of
The thorium and actinium chains can be followed on the diagrams in the same manner, but in the case of actinium the parent elements are not satisfactorily settled so that the atomic weights in this series are all doubtful.
the actinium  series. Disregarding  this  for  the  moment  and
following  the  main  chain,  92  per  cent,  of  the  atoms  of  uranium=


==10. The Atomic Weight of Lead==


The theory of Isotopes of which Professor Soddy had proved himself so prominent an advocate and defender, received its most triumphant vindication, as far as it concerned the products of radioactivity, at the hands of the very chemists who had most reason to doubt its general apphcation, the specialists in the determination of atomic weights.


1  Darwin, Nature, 106,  82,    1920.
The charts of radioactive disintegration<ref>P. 14.</ref> show that the final product of every series is lead. If we take the main chain of the uranium-radium transformation this lead must have an atomic weight 206, for it has lost 5 alpha particles – each of weight 4 – since it was radium, and the atomic weight of radium is 226. On the other hand if we take the main thorium chain the lead end product must be 6 alpha particles lighter than thorium (232.15) and so should have an atomic weight about 208.


Now ordinary lead, from non-radioactive sources has an atomic weight 207.20, so Soddy<ref>1 Soddy, ''Ann. Rep. Chem. Soc'', '''269''', 1913.</ref> suggested in 1913 that the lead derived from minerals containing uranium but no thorium might have a smaller atomic weight than ordinary lead, and on the other hand the atomic weight of lead from minerals containing thorium but no uranium might be greater.


16  ISOTOPES
The first experiments were made by Soddy and Hyman<ref>2 Soddy and Hyman, ''Trans. Chem. Soc'', '''105''', 1402, 1914.</ref> with a very small quantity of lead from Ceylon Thorite. This gave a perceptibly higher atomic weight than ordinary lead. Later a large quantity of the same mineral was available. The lead from this when carefully purified gave a density 0'26 per cent, higher than that of common lead. On the assumption that the atomic volumes of isotopes are equal this figure corresponds to an atomic weight of 207.74. A chemical atomic weight determination gave 207-694. A sample of the same lead was sent to Vienna where Professor [[wikipedia:Otto Hönigschmid|Honigschmid]], a well known expert in such matters, obtained from it a value 207.77 as a mean of eight determinations. These figures not only showed that thorium lead had a higher atomic weight than ordinary lead but also that their atomic volumes were identical, as expected from theory.<ref>Soddy, ''Roy. Ins.'', May 18, 1917.</ref>


II  suffer  an  a  ray  change  and  are  transformed  into  ionium,,
At the same time as this work was in progress, the leading American authority on atomic weights, [[wikipedia:Theodore William Richards|T. W. Richards]] of Harvard, started a series of investigations on lead derived from various radioactive minerals.<ref>Richards and Lembert, ''J. Amer. Chem. Soc'', ''36'', 1329, 1914. [{{doi}}10.1021/ja02184a001] </ref> The samples of lead from uranium minerals all gave results lower than ordinary lead, as was expected, and one particularly pure specimen of uraniolead from Norwegian cleveite gave 206.08,<ref>5 Richards and Wadsworth, J. Amer. Chem. Soc, 38, 2613,  1916.</ref> a very striking agreement with theory. The following table of properties is taken from his Presidential address to the American Association at Baltimore, December, 1918.
atomic  weight  230,  atomic  number  90.  Ionium  loses  an  a
particle  and  becomes  radium,  atomic  weight  226.  This  by
the  same  process  changes  to  radium  emanation,  then  to  radium
A,  and  then  to  radium  B  with  atomic  weight  214,  We  see
that  uranium  II  has  lost  5  a  particles  in  succession,  thereby-
coming  back  10  places,  92-82  in  the  periodic  table,  and  its
atomic  weight  has  been  reduced  20  units  in  the  process.
Radium  B  loses  a  ^  particle,  becoming  radium  C  which  can
disintegrate  in  two  different  ways.  An  extremely  small  pro-
portion, 0-03  per  cent.,  of  its  atoms  undergo  an  a  ray  change  to=
 
radium  C2  which  then  loses  a  ^  particle  and  may  become  inactive=
 
lead  of  atomic  weight  210.  The  vast  majority  of  the  atoms  of
radium  C  lose  a  ^  particle  and  form  radium  C.  This  next
loses  an  a  particle  and  becomes  radium  D,  an  active  isotope
of  lead  of  atomic  weight  210.  Radium  D  now  loses  two  ^
particles  in  succession,  becoming  radium  E  and  then  radium  E,
which  is  also  called  polonium.  This  finally  undergoes  its  last
a  ray  change  and  becomes  inactive  uranium  lead  of  atomic
weight  206.
 
The  thorium  and  actinium  chains  can  be  followed  on  the  dia-
grams in  the  same  manner,  but  in  the  case  of  actinium  the
parent  elements  are  not  satisfactorily  settled  so  that  the
atomic  weights  in  this  series  are  all  doubtful.
 
===10.  The  Atomic  Weight  of  Lead=== 
The  theory  of  Isotopes
of  which  Professor  Soddy  had  proved  himself  so  prominent
an  advocate  and  defender,  received  its  most  triumphant
vindication,  as  far  as  it  concerned  the  products  of  radio-
activity, at  the  hands  of  the  very  chemists  who  had  most
reason  to  doubt  its  general  apphcation,  the  specialists  in  the
determination  of  atomic  weights.
 
The  charts  of  radioactive  disintegration  ^  show  that  the  final
product  of  every  series  is  lead.  If  we  take  the  main  chain
of  the  uranium -radium  transformation  this  lead  must  have  an
atomic  weight  206,  for  it  has  lost  5  alpha  particles  eac=
h  of
weight  4  since  it  was  radium,  and  the  atomic  weight  of  =
radium
is  226.    On  the  other  hand  if  we  take  the  main  thorium  chain=
 
 
1  P.  14.
 
 
THE  RADIOACTIVE  ISOTOPES  17
 
the  lead  end  product  must  be  6  alpha  particles  lighter  than
thorium  (232-15)  and  so  should  have  an  atomic  weight  about
-08.
 
Now  ordinary  lead,  from  non-radioactive  sources  has  an
atomic  weight  207*20,  so  Soddy  ^  suggested  in  1913  that  the
lead  derived  from  minerals  containing  uranium  but  no  thorium
might  have  a  smaller  atomic  weight  than  ordinary  lead,  and
on  the  other  hand  the  atomic  weight  of  lead  from  minerals
containing  thorium  but  no  uranium  might  be  greater.
 
The  first  experiments  were  made  by  Soddy  and  Hyman  ^
with  a  very  small  quantity  of  lead  from  Ceylon  Thorite.  This
gave  a  perceptibly  higher  atomic  weight  than  ordinary  lead.
Later  a  large  quantity  of  the  same  mineral  was  available.
The  lead  from  this  when  carefully  purified  gave  a  density
0'26  per  cent,  higher  than  that  of  common  lead.  On  the
assumption  that  the  atomic  volumes  of  isotopes  are  equal
this  figure  corresponds  to  an  atomic  weight  of  207-74.  A  chem-
ical atomic  weight  determination  gave  207-694.  A  sample  of
the  same  lead  was  sent  to  Vienna  where  Professor  Honigschmid,
a  well  known  expert  in  such  matters,  obtained  from  it  a  value
207-77  as  a  mean  of  eight  determinations.  These  figures  not
only  showed  that  thorium  lead  had  a  higher  atomic  weight
than  ordinary  lead  but  also  that  their  atomic  volimies  were
identical,  as  expected  from  theory .^
 
At the same time as this work was in progress, the leading
American authority on atomic weights, T. W. Richards of
Harvard, started a series of investigations on lead derived from=
 
various radioactive minerals.*  The samples of lead from
uranium minerals all gave results lower than ordinary lead,
as was expected, and one particularly pure specimen of uranio-
lead  from Norwegian cleveite gave 206-08,^  a very strildng
agreement with theory. The follomng  table of properties
is taken from his Presidential address to the American
Association at Baltimore, December, 1918.
 
1  Soddy,  Ann.  Rep.  Chem.  Soc,  269,    1913.
 
2  Soddy  and  Hyman,  Trans.  Chem.  Soc,  105,  1402,    1914.
 
3  Soddy,  Roy.  Ins.,  May  18,  1917.
 
*  Richards  and  Lembert,  J.  Amer.  Chem.  Soc,  36,  1329,    1914.
5  Richards  and  Wadsworth,  J.  Amer.  Chem.  Soc,  38,  2613,    1916.=




Line 620: Line 108:
|}
|}


In further confirmation Maurice Curie in Paris reported
In further confirmation [[wikipedia:Maurice Curie|Maurice Curie]] in Paris<ref>M. Curie, ''Compt. Bend.'', '''158''', 1676, 1914.</ref> reported 206.36 for a lead from carnotite, and a still lower figure, 206.046, was obtained by Honigschmid in Vienna for a lead from the very pure crystalised pitchblende from Morogoro. This is the lowest atomic weight found so far. The highest, 207.9, was also determined by Honigschmid for lead from Norwegian thorite.<ref>Honigschmid, ''Zeit. Elektrochem.'', '''24''', 163, 1918 ; '''25''', 91, 1919.</ref>
206-36 for a lead from carnotite, and a still lower figure, 206-=
046,
was obtained by Honigschmid in Vienna for a lead from the
very pure crystalhsed  pitchblende from Morogoro. This is
the lowest atomic weight found so far. The highest, 207-9,
was also determined by Honigschmid for lead from Norwegian
thorite.2


===11. Atomic weights of Thorium and Ionium=== 
==11. Atomic weights of Thorium and Ionium==
Although
the  above  results  obtained  with  lead  are  far  the  most  con-
clusive and  important  it  is  not  the  only  element  which  affords
direct  experimental  evidence  of  the  different  atomic  weights
of  isotopes.  The  atomic  weight  of  ionium,  calculated  by
adding  the  weight  of  one  alpha  particle  to  the  atomic  weight
of  its  product,  radium,  is  230,  whereas  that  of  thorium,  its
isotope,  is  slightly  above  232.  Joachimsthal  pitchblende  con-
tains hardly  any  thorium  so  that  an  ionium-thorium  prepara-
tion separated  by  Auer  von  Welsbach  from  30  tons  of  this
mineral  might  be  regarded  as  containing  a  maximum  concen-
tration of  ionium.  On  the  other  hand  the  period  of  thorium
is  about  10^  times  longer  than  that  of  ionium  so  that  it  was
doubtful  if  even  in  this  preparation  there  would  be  enough
ionium  to  show  a  difference  in  atomic  weight.  Honigschmid
and  Mile.  Horovitz  have  made  a  special  examination  of  this
point,  first  redetermining  as  accurately  as  possible  the  atomic
weight  of  thorium  and  then  that  of  the  thorium -ionium  prepar-


iM. Curie, Compt. Bend., 158, 1676,    1914.
Although the above results obtained with lead are far the most conclusive and important it is not the only element which affords direct experimental evidence of the different atomic weights of isotopes. The atomic weight of ionium, calculated by adding the weight of one alpha particle to the atomic weight of its product, radium, is 230, whereas that of thorium, its isotope, is slightly above 232. Joachimsthal pitchblende contains hardly any thorium so that an ionium-thorium preparation separated by Auer von Welsbach from 30 tons of this mineral might be regarded as containing a maximum concentration of ionium. On the other hand the period of thorium is about 10<sup>5</sup> times longer than that of ionium so that it was doubtful if even in this preparation there would be enough ionium to show a difference in atomic weight. Honigschmid and Mlle. [[wikipedia:Stefanie Horovitz|Horovitz]] have made a special examination of this point, first redetermining as accurately as possible the atomic weight of thorium and then that of the thorium-ionium preparation from pitchblende. They found 232.12 for the atomic weight of thorium, and by the same careful method 231.51 for that of the thorium-ionium.


Honigschmid,  Zeit. Elektrochem. ,  24,  163,    1918  ;  25,  9=
==12. Use of radioactive isotopes as indicators==
1,    1919.


Consider an inactive element A which has a radioactive isotope B. If these are mixed together in any proportions no chemical or physical process known is capable of altering the ratio of the proportions of this mixture to any measurable extent. Now the radioactive methods of detecting and measuring B are many millions of millions of times more delicate than the chemical methods of detecting and measuring A, so that by mixing with A a small quantity of B we can trace its presence far beyond the limits of chemical analysis. We have, as it were, marked the atoms of A with an indelible label so that the minutest trace of the element can be measured with ease and certainty.


THE  RADIOACTIVE  ISOTOPES 19
By this powerful and novel device, which has been developed by G. Hevesy<ref>Hevesy, ''Brit. Assoc'', 1913 ; ''Chem. News'', Oct. 13, 166, 1913.</ref> 10<sup>-9</sup> gr. of lead can be determined quantitatively and solution concentrations can be dealt with down to 10<sup>-14</sup> of normal. By adding radium D to the lead salt and estimating it electroscopically the solubility of lead sulphide and chromate, and the amount of lead chloride carried down in a silver chloride precipitate, may readily be determined.


ation  from  pitchblende. They  found  232-12  for  the atomic
Recently, by the same principle, it has been shown that a free exchange of the metallic atom among the competing acid radicles occurs for ionised, but not for non-ionised, compounds. The general method was to mix solutions of two different compounds of lead in equimolecular proportions, the one compound only being "activated" by presence of thorium-B (which is isotopic with lead), and to determine the activity of the lead in the less soluble compound crystallising out. When active lead nitrate and inactive lead chloride are dissolved in molecular proportion in boiling pyridine, the lead in the lead chloride crystalHsing out is half as active as the lead in the original lead nitrate, but when such an active lead salt is so mixed with an organic compound of lead, such as lead tetraphenyl or diphenyl nitrate, in suitable solvents, no interchange of lead occurs, and the active lead salt retains its original activity. This constitutes something like a direct proof of the ionic dissociation theory and of the current views as to the difference between the nature of chemical union in electrolytes and non-electrolytes. When the acetates of quadrivalent activated lead and of bivalent inactive lead are mixed in glacial acetic acid, the activity of the first compound, after crystallising out from the mixture, is reduced to one half. This indicates, since the two lead ions differ only by two electrons, a free interchange of electrons between them and a dynamic equilibrium between ions and electrons and between free electrons and the electrodes in electrolysis.<ref>G. Hevesy and L. Zechmeister, ''Ber''., '''53B''', 410, 1920 ; ''Zeitsch. Elektrochem.'' '''26''', 151, 1920.</ref>
weight  of thorium, and by  the same  careful  method  231*51
for  that  of the thorium -ionium.


===12. Use  of radioactive isotopes  as  indicators===
Isotopes can also be used to determine the velocity of diffusion of molecules among themselves.<ref>J. Groh and Hevesy, ''Ann. Physik.'', iv., '''63''', 85,  1920.</ref> The rate of diffusion is dependent on the molecular diameter, and not on the mass, so that a radioactive element diffusing among the inactive molecules of its isotope affords a means of investigating this otherwise insoluble problem. The experiment has been tried with molten lead. At the bottom of a narrow vertical tube was placed a layer of lead rendered active by the presence of thorium-B, and above it a layer three times the height of common lead. The whole was kept at 340&deg; for several days. After cooling, the cylinder was cut into four equal lengths, each melted and hammered into foil, and the concentration of thorium-B in each determined by alpha ray measurements. Values for the diffusion coefficient between 1.77 and 2.54 per sq. cm. per day, with a mean of 222 in seventeen experiments, were obtained. On certain theories of physical chemistry this corresponds with a diameter of the lead molecule between 0.78 and I1.16 x 10<sup>-8</sup> cm., according to the formulae used to connect the two quantities. The value found by similar theories when reduced to a temperature of 18&deg; and for a fluid of the viscosity of water, becomes 2.13. Since the value for lead ions diffusing in aqueous solutions is 0.68, this indicates that the molecular diameter in the case of metallic lead is only a third of that in the case of the ion, and shows that the latter is probably hydrated.<ref>Soddy, Ann. Rep. Chem. Soc, 227, 1920.</ref>
Consider an  inactive element  A  which  has a radioactive  isotope  B.
If  these  are  mixed  togeth
==CHAPTER  II - THE  RADIOACTIVE  ISOTOPES=
==5. Chemical identities among the radioactive elements=
Apart from the purely speculative considerations
which have aheady been detailed, the theory of isotopes had
its birth in the gigantic forward wave of human knowledge
inaugurated by the discovery of radioactivity. It can admittedly be argued that, even if no radioactive elements existed,
isotopes would inevitably have been discovered by the method
of positive rays. But progress must then have been exceedingly slow, and the arrival at the real interpretation of the idea,
depending as it does on Sir [[wikipedia:Ernest Rutherford|Ernest Rutherford]]'s theory of
the " nucleus" atom, almost impossible.


In 1906 [[wikipedia:Bertram Boltwood|Boltwood]] at Yale discovered a new element in the
==13. Classification of the radioactive isotopes==
radioactive group which he called [[wiktionary:ionium|Ionium]],<ref>Boltwood, ''Amer. J. Sci'', '''22''', 537, 1906;[https://www.proquest.com/docview/89598254?pq-origsite=gscholar&fromopenview=true&sourcetype=Scholarly%20Journals] '''24''', 370, 1907.[https://www.proquest.com/docview/89598004/fulltextPDF/1D7013FDBDF94219PQ/1?accountid=12154&sourcetype=Scholarly%20Journals]</ref> and described
as having chemical properties similar to those of thorium.
So much was this the case that if, by accident, salts of these
two elements were mixed, he found it impossible to separate
them again by any of the chemical processes.


Boltwood, being occupied in the experimental proof that
It is clear that the relations between isotopes formed by radioactive
ionium was the parent substance of radium, did not pursue
disintegrations need not necessarily have the same simple form as those subsisting between isotopes of the inactive elements. Neuberger,<ref>Neuburger, Nature, 108, 180, 1921.</ref> using the nucleus model of the radioelements proposed by Lise Meitner,<ref>Meitner, ''Die Naturwissenschaften'', '''9''', 423, 1921. </ref> suggests that the radioactive isotopes may be divided into three or even four classes.
this line of investigation further at the time, but the work
was later taken in hand by Marckwald and Keetman of Berlin.<ref>Keetman, ''Jahr. Radioactivitat'', '''6''', 269, 1909.</ref> Thanks to the rapid advance in radioactive methods there
were now at command means of detecting change in concentration of a delicacy unheard of in the previous work on the
rare earths, but yet, after years of patient and laborious work,
not the slightest sign of separation of ionium and thorium
could be observed. The chemical similarity between these
two bodies was therefore of an order entirely different to that
exhibited by the rare earth elements, and came as near absolute
identity as the most critical mind could require.


This result was confirmed in the most rigorous manner by
:(1) Isotopes of the first class are those which possess only the same nuclear charge and the same arrangement of outer electrons such as radium and mesothorium I.
[[wikipedia:Carl Auer von Welsbach|Auer v. Welsbach]]<ref>A. von Welsbach, ''Wien. Ber.'' iia, 119, 1011,  1910.</ref> who was able to apply to the problem
his valuable experience in work on the rare earths.


Furthermore, [[wiktionary:mesothorium|Mesothorium]], discovered by Hahn in 1907,
:(2) Isotopes of the second class have, in addition, the same nuclear mass, that is to say the same atomic weight, and the same total number of nuclear "building stones." Examples of this class are ionium and uranium Y.
was shown to be chemically inseparable from radium by
Marckwald<ref>Marckwald, ''Ber. d. Chem. Oes.'', '''40''', 3420, 1910.</ref> and Soddy<ref>Soddy, ''Trans. Chem. Soc'', '''99''', 72, 1911.</ref> and similar chemical identities were
shown to be exceedingly probable in many other cases of
radioactive products. Certain regularities in the occurrence
of these were pointed out by [[wikipedia:Otto Hahn|Hahn]] and [[wikipedia:Lise Meitner|Meitner]].<ref>Hahn and Meitner, ''Physikal. Zeitsch.'', '''11''', 493, 1910.</ref>


The situation was admirably summed up by Soddy in his
:(3) Isotopes of the third class still possess the same number of each nuclear building stone, but they have a different arrangement of these in the atomic nucleus, and thus possess different chances of disintegrating, such as Radium D and Actinium B.
report on radioactivity for the year 1910<ref>Soddy, ''Chem. Soc. Ann. Rep.'', '''285''', 1910.</ref> in the following words:


"These regularities may prove to be the beginning of some
:(4) Isotopes of the fourth class would be those possessing the same arrangement of nuclear building stones in the atomic nucleus, and thus the same probability of disintegrating. Such isotopes actually exist, but we have no available means of distinguishing between them. Hence we cannot at present designate them definitely as isotopes. Examples of these are radium C<sub>2</sub> and actinium D.
embracing generalisation, which will throw light, not only on
radioactive processes, but on elements in general and the
Periodic Law. Of course, the evidence of chemical identity
is not of equal weight for all the preceding cases, but the
complete identity of ionium, thorium and radiothorium, of
radium and mesothorium 1, of lead and radium D, may be
considered thoroughly established. . . . The recognition
that elements of different atomic weights may possess identical
properties seems destined to have its most important apphcation in the region of inactive elements, where the absence of
a second radioactive nature makes it impossible for chemical
identity to be individually detected. Chemical homogeneity
is no longer a guarantee that any supposed element is not a
mixture of several of different atomic weights, or that any
atomic weight is not merely a mean number. The constancy
of atomic weight, whatever the source of the material, is not
a complete proof of homogeneity, for, as in the radioelements,
genetic relationships might have resulted in an initial constancy
of proportion between the several individuals, which no subsequent natural or artificial chemical process would be able to
disturb. If this is the case, the absence of simple numerical
relationships between the atomic weights becomes a matter of
course rather than one of surprise."


===6. Spectroscopic identity of isotopes===
==References==
The next great
advance was of an even more revolutionary character. This
consisted in the demonstration that the chemically indistinguishable products of the transformation of the radioactive
elements might also be spectroscopically identical. The idea
that elements of different atomic weight might yet have the
same spectrum originated in Sir Ernest Rutherford's laboratory
and appears to have been first entertained by A. S. Russell.
With Rossi ^ he undertook the comparison between the spectrum of pure thorium and that of a mixture of thorium and
ionium which radioactive evidence showed to contain a large
percentage of the latter element. No new fines attributable
to ionium were observed ; in fact the spectra obtained were
absolutely  indistinguishable.
 
After giving in full the radioactive evidence as to the probable
percentage of ionium present, and showing that it was practically impossible for this to be too small for its spectrum to
appear, the writers go on as foUows :
 
" There are, however, two other possible ways of explaining
our failure to obtain a distinct spectrum for ionium, besides the
one discussed above.  It is possible that :
 
" (1) Ionium has no arc spectrum in the region investigated,
or
 
" (2) Ionium and thorium have identical spectra in the region
investigated.
 
" The first possibifity is highly improbable, for all solids of
high atomic weights have arc spectra, and, further, aU rare
earths have highly comphcated spectra.
 
" The second possibifity, though somewhat speculative
in nature, is suggested by some recent work on the chemical
properties of the radio-elements. There is no evidence
at present to disprove its truth. It is well known that there
are no less than four sets of longfived radio-elements, the
 
1 Russell and Rossi, Proc. Roy. Soc, 77A, 478,  1912.
 
 
10 ISOTOPES
 
members of each of which are chemically non-separable. These
elements do not all belong to the group of rare earths, many
non-radioactive members of which are known to be chemically
very similar. Mesothorium, for instance, which is chemically
non-separable ' from radium, belongs to the alkahne earth
group. Again the two non-separable a ray products which
are present in ordinary uranium, and which have been called
by Geiger and Nuttall uranium I and uranium II belong to
the chromium-molybdenum-tungsten group of elements. The
explanation of these striking chemical similarities is very
probably that the two very similar bodies are really different
members of the same group of elements, the difference in their
chemical properties being less pronounced than the difference
between other members of the same group, owing to the small
difference in their atomic weights. But the possibility that
they are identical in all physical and chemical properties, and
differ only in atomic weight and in radioactive properties, should
not be lost sight of. If this explanation should eventually prove
justified, the spectrum of ionium would he identical with that of
thorium."
 
It is not surprising that the idea was put forward with some
caution. Unhke that of chemical identity which had been
led up to by a gradual series of steps, it was entirely new and
contrary to all the preconceived ideas of the relations between
the spectrum of an element and the masses of its atoms. The
new departure was supported by Soddy ^ but received some
adverse criticism on the ground of insufficient evidence. The
later work bearing on this point will be described in Chapter X.
 
Ah-eady in 1911 the theory of the " Nucleus Atom " 2 had
been formulated. This gave the first hint as to the physical
meaning of chemical and spectroscopic identity, namely that
the nuclei of atoms might vary in their mass but yet, at the
same time, possess some property in common with each other,
namely nuclear charge, upon which the chemistry and spectra
depend.
 
In  1912 appeared the electrochemical work of  Hevesy,*
 
1 Soddy, Chem. News, Feb. 28, 1913. * F. p. 92.
 
3 G. Hevesy, Phil. Mag., 23, 628, 1912 ; Physikal. Zeitsch. 15,  672,
715,  1912.
 
 
THE RADIOACTIVE ISOTOPES 11
 
which led to the discovery of the remarkable field of research
opened up by the use of radioactive bodies as indicators.^ A
Httle later Paneth and Hevesy were able to show the complete
identity of the electrochemical properties of Radium D and
Lead.2
 
In 1914 Rutherford and Andrade ^ examined the self -excited
X-ray spectrum of radium B. They used a crystal of rock
salt for the analysis and got rid of the effect of the swift ^
rays by putting the source in a strong magnetic field. The wave
length of the L radiation proved to be exactly that expected
for lead from Moseley's experiment.* This was the first
proof that isotopes had identical X-ray spectra. The actual
values for ordinary lead were subsequently determined by
Siegbahn and found to be in excellent agreement with Rutherford and Andrade's results.
 
===7. The Chemical Law of Radioactive change==This
law, put in the briefest form, asserts : A radioactive element
when it loses an alpha particle goes back two places in the
Periodic Table ; when it loses a beta particle it goes forward
one place.
 
The law has been associated with the name of Soddy ^ who
was the first to suggest, in the form of a valency property,
that part of it relating to alpha rays.^ But in its more complete enunciation, which took place early in 1913, at least
four other investigators can claim a share.
 
RusseU was the first to pubhsh a law covering both Idnds of
rays,' but owing to the fact that he failed to reaHse that the
sequence of elements in the periodic table is a continuous expression, his statement was not so simple and definite as it might
have been.  Fajans,^ using as foundation the electrochemical
 
^ F. p. 19.
 
2 Paneth and Hevesy, Sitzungber. K. Akad. Wiss. Wien, iiA, 123,
1037,  1913.
 
3 Rutherford and Andrade, Phil. Mag. 27, 854, 1914.    * V. p. 93.
 
^ V. Stewart, Recent Advances in Physical and Inorganic Chemistry,
Longmans, 1919.
 
^ Soddy, The Chemistry of the Radio Elements, 29, First Edition,
Longmans,  1911.
 
' Russell, Chem. News, Jan, 31, 1913,
 
8 Fajans, Physikal. Zeitsch. Feb.  15, 1913.
 
 
12 ISOTOPES
 
results of Hevesy,^ and Soddy, working on the results of a
very full chemical investigation carried out at his request by
Fleck, 2 pubUshed the generalisation in its full and complete
form independently, and practically at the same time.
 
This law, which will be shown later to be a natural consequence of the much wider generahsation discovered by Moseley,^
has been of the greatest value in correlating the numerous
products of radioactive change, and predicting with accuracy
which of them mil have identical properties. To the latter
the name Isotopes was apphed by Soddy in the following
words : " The same algebraic sum of the positive and
negative charges in the nucleus when the arithmetical sum
is different gives what I call ' isotopes ' or ' isotopic elements '
because they occupy the same place in the periodic table.
They are chemically identical, and save only as regards the
relatively few physical properties which depend upon atomic
mass directly, physically identical also." Any element which
is the result of a series of changes involving the loss of twice
as many beta particles as alpha particles must clearly be the
isotope of the parent element, since it must inevitably, by the
above law, reach the same place in the periodic table at the end
of these operations.
 
===8. Isobares===
Just as we can have elements of the same
chemical properties but different atomic weight so we can also
have those with the same atomic weight but different chemical
properties. These Stewart * has called " Isobares." Any
product due to the loss of a beta ray (which has a negligible
mass) 5 must be an isobare of its parent substance, for, without
change of mass, it has moved in the periodic table and so
changed its chemical properties. It is interesting to note in
this connection that no isobare has actually been discovered
among the non-radioactive elements as yet, but they must
certainly exist.*'
 
^ Hevesy, Physihal. Zeitsch. Jan.  15,  1913.
 
2 Fleck, Trans. Chem. Soc. 103, 381,  1052,  1913.
 
3 V. p. 93.
 
* Stewart, Phil. Mag. 36, 326,  1918.
' V. p. 91.
V. p. 77.
 
 
THE RADIOACTIVE ISOTOPES 13
 
===9. The Radioactive Transformations===
The radioactive
elements are all formed from the two parent elements inanium
and thorium by a series of changes or transformations. These
changes can be classified according to their nature into two
types. In the first type of change called the a ray change
the atom loses a particle of mass 4 carrying two positive
charges {+ 2e) which has been identified with the nucleus
of the helium atom.^ In the second or ^ ray change the
particle shot off has a neghgible mass and carries a single
negative charge (  e). Hence in an a ray change the element loses 4 units in atomic weight, while in a /3 ray change
its weight is unaltered.
 
The rate of decay of an element is measured by the " half
value " period which may vary from 10^=C2=B0 years to 10 ~^^ of  a
second. The velocity with which the rays are ejected also
varies and is apparently connected with the period of the
element by the very interesting relation of Geiger and NuttaU.^
The intricate researches by which the complex series of transformations have been explained belong to the subject of
Radioactivity and cannot be described here. From the point
of view of isotopes it will be enough to consider the final
results which are given in the two diagrams (Figs. 1 and 2).
 
In the first of these, which is due to Soddy,^ the nuclear
charge or Atomic number,'* upon which all the chemical
and spectroscopic properties of the elements depend, and
which expresses its position in the periodic table, is indicated
by a series of columns edged with thick fines sloping downwards to the right. The atomic weights are shown by fine
lines sloping in the opposite direction. The fines corresponding to even atomic weights have been omitted to simpfify
the scheme. AU elements lying in the same column will
therefore be isotopes and all elements lying on the same fine
sloping up to the right will be isobares. The a and ^ ray
changes are shown by arrows and the period of decay of the
elements indicated by times expressed in suitable units.
 
1 V. Table p. 106.
 
* Rutherford, Radioactive Substances and their Radiations, p. 607,
Cambridge, 1913.
 
3 Soddy, Trans. Chem. Soc, U5, 16,  1919. * V. p. 93.
 
 
14
 
 
ISOTOPES
 
 
Fig. 1. Diagram of the transformations of the radio-elements showing
atomic number, atomic weight and period of disintegration of each
product.
 
 
THE RADIOACTIVE ISOTOPES
 
 
16
 
 
The second diagram ^ is arranged in a simple manner to
show the general chains of transformation at a glance. In it
the a and /5 ray changes are plotted against atomic number
and the other information omitted. On this diagram all
elements lying on the same horizontal level will be isotopes.
To take an example, uranium I which has an atomic number
92 and an atomic weight 238 loses one a particle and becomes
uranium X, atomic number 90, atomic weight 234, This then
gives off two /3 rays in succession, first becoming uranium X2
 
 
Uranium  U.ji
 
 
Profoachnium
 
 
U.x,  Ionium  U.Y  \  Rac/ioact.    Thorium Radioth.
j Actinium Mikj^
 
 
Racfu
 
 
Ra. Emanation
 
 
Polonium    RaC    Ra.A AcC^
 
Ral/  R^.C
 
 
AcX Mesoth.j  Th'.X
 
 
A C.Em.
 
 
Tti.Em.
 
 
Ac. A
 
 
Ra.D Pb
\
Ra.
 
 
\
 
 
Ra.B    Pb  Pb.
 
 
AcC
\
 
 
\
 
 
n.Ci
/ \
 
 
TfiA
 
 
Ac.D
 
 
Ac.B    P6.  P6.
 
 
ThC
 
 
Tfy.B
 
 
Th.D
 
 
92
 
91
 
90
 
89
 
^Z
 
87
 
86
 
85
 
84
 
83
 
82
 
81
 
[[File:Aston 1922 Figure 2.jpg|thumb|600 px|Fig. 2. Diagram of the radioactive transformations in relation to atomic
numbers. In every case a step two downwards is accompanied by the
emission of an a particle and one downwards by a &beta; particle.]]
 
and then Uranium II. Uranium II has an atomic number
92 so that it is an isotope of uranium I. It has an atomic
weight 234 so it is anisobare of uranium Xi and uranium X2.
Uranium II can disintegrate by shooting off an a particle in
two different ways ; about 8 per cent, of its atoms appear to
form uranium Y, which is probably the parent substance of
the actinium series. Disregarding this for the moment and
following the main chain, 92 per cent, of the atoms of uranium
 
 
1 Darwin, Nature, 106, 82,  1920.
 
 
16 ISOTOPES
 
II suffer an a ray change and are transformed into ionium,,
atomic weight 230, atomic number 90. Ionium loses an a
particle and becomes radium, atomic weight 226. This by
the same process changes to radium emanation, then to radium
A, and then to radium B with atomic weight 214, We see
that uranium II has lost 5 a particles in succession, therebycoming back 10 places, 92-82 in the periodic table, and its
atomic weight has been reduced 20 units in the process.
Radium B loses a ^ particle, becoming radium C which can
disintegrate in two different ways. An extremely small proportion, 0-03 per cent., of its atoms undergo an a ray change to
radium C2 which then loses a ^ particle and may become inactive
lead of atomic weight 210. The vast majority of the atoms of
radium C lose a ^ particle and form radium C. This next
loses an a particle and becomes radium D, an active isotope
of lead of atomic weight 210. Radium D now loses two ^
particles in succession, becoming radium E and then radium E,
which is also called polonium. This finally undergoes its last
a ray change and becomes inactive uranium lead of atomic
weight 206.
 
The thorium and actinium chains can be followed on the diagrams in the same manner, but in the case of actinium the
parent elements are not satisfactorily settled so that the
atomic weights in this series are all doubtful.
 
===10. The Atomic Weight of Lead===
The theory of Isotopes
of which Professor Soddy had proved himself so prominent
an advocate and defender, received its most triumphant
vindication, as far as it concerned the products of radioactivity, at the hands of the very chemists who had most
reason to doubt its general apphcation, the specialists in the
determination of atomic weights.
 
The charts of radioactive disintegration ^ show that the final
product of every series is lead. If we take the main chain
of the uranium -radium transformation this lead must have an
atomic weight 206, for it has lost 5 alpha particles each of
weight 4 since it was radium, and the atomic weight of radium
is 226.  On the other hand if we take the main thorium chain
 
1 P. 14.
 
 
THE  RADIOACTIVE ISOTOPES 17
 
the lead end product must be 6 alpha particles lighter than
thorium (232-15) and so should have an atomic weight about
-08.
 
Now ordinary lead, from non-radioactive sources has an
atomic weight 207*20, so Soddy ^ suggested in 1913 that the
lead derived from minerals containing uranium but no thorium
might have a smaller atomic weight than ordinary lead, and
on the other hand the atomic weight of lead from minerals
containing thorium but no uranium might be greater.
 
The first experiments were made by Soddy and Hyman ^
with a very small quantity of lead from Ceylon Thorite. This
gave a perceptibly higher atomic weight than ordinary lead.
Later a large quantity of the same mineral was available.
The lead from this when carefully purified gave a density
0'26 per cent, higher than that of common lead. On the
assumption that the atomic volumes of isotopes are equal
this figure corresponds to an atomic weight of 207-74. A chemical atomic weight determination gave 207-694. A sample of
the same lead was sent to Vienna where Professor Honigschmid,
a well known expert in such matters, obtained from it a value
207-77 as a mean of eight determinations. These figures not
only showed that thorium lead had a higher atomic weight
than ordinary lead but also that their atomic volimies were
identical, as expected from theory .^
 
At the same time as this work was in progress, the leading
American authority on atomic weights, T. W. Richards of
Harvard, started a series of investigations on lead derived from
various radioactive minerals.* The samples of lead from
uranium minerals all gave results lower than ordinary lead,
as was expected, and one particularly pure specimen of uraniolead from Norwegian cleveite gave 206-08,^ a very strildng
agreement with theory. The follomng table of properties
is taken from his Presidential address to the American
Association at Baltimore, December, 1918.
 
1 Soddy, Ann. Rep. Chem. Soc, 269,  1913.
 
2 Soddy and Hyman, Trans. Chem. Soc, 105, 1402,  1914.
 
3 Soddy, Roy. Ins., May 18, 1917.
 
* Richards and Lembert, J. Amer. Chem. Soc, 36, 1329,  1914.
5 Richards and Wadsworth, J. Amer. Chem. Soc, 38, 2613,  1916.


{| class="wikitable"
! !! Common Lead!! Mixture Australian !! Uranio-Lead !! \multicolumn{2}{c|Percentage Difference
|| || A || B || C || A--B || A--C
|| Atomic weight || 207.19 || 206.34 || 206.08 || 0.42 || 0.54
|| Density || 11.337 || 11.280 || 11.273 || 0.42 || 0.56
|| Atomic volume || 18.277 || 18.278 || 18.281 || 0.01 || 0.02
|| Melting point (absolute) || 600.53 || 600.59 || --- || 0.01 || --|| Solubility (of nitrate) || 37.281 || 37.130 || --- || 0.41 || --|| Refractive Index (nitrate) || 1.7815 || 1.7814 || --- || 0.01 || --|| Thermoelectric effect || --- || --- || --- || 0.00 || --|| Spectrum wave-length || --- || --- || --- || 0.00 || 0.00
|}
In further confirmation Maurice Curie in Paris reported
206-36 for a lead from carnotite, and a still lower figure, 206-046,
was obtained by Honigschmid in Vienna for a lead from the
very pure crystalhsed pitchblende from Morogoro. This is
the lowest atomic weight found so far. The highest, 207-9,
was also determined by Honigschmid for lead from Norwegian
thorite.2
===11. Atomic weights of Thorium and Ionium===
Although
the above results obtained with lead are far the most conclusive and important it is not the only element which affords
direct experimental evidence of the different atomic weights
of isotopes. The atomic weight of ionium, calculated by
adding the weight of one alpha particle to the atomic weight
of its product, radium, is 230, whereas that of thorium, its
isotope, is slightly above 232. Joachimsthal pitchblende contains hardly any thorium so that an ionium-thorium preparation separated by Auer von Welsbach from 30 tons of this
mineral might be regarded as containing a maximum concentration of ionium. On the other hand the period of thorium
is about 10^ times longer than that of ionium so that it was
doubtful if even in this preparation there would be enough
ionium to show a difference in atomic weight. Honigschmid
and Mile. Horovitz have made a special examination of this
point, first redetermining as accurately as possible the atomic
weight of thorium and then that of the thorium -ionium prepar
iM. Curie, Compt. Bend., 158, 1676,  1914.
Honigschmid, Zeit. Elektrochem. , 24, 163,  1918 ; 25, 91,  1919.
THE  RADIOACTIVE  ISOTOPES 19
ation from pitchblende. They found 232-12 for the atomic
weight of thorium, and by the same careful method 231*51
for that of the thorium -ionium.
===12. Use of radioactive isotopes as indicators===
Consider an inactive element A which has a radioactive isotope B.
If these are mixed together in any proportions no chemical
or physical process known is capable of altering the ratio of
the proportions of this mixture to any measurable extent.
Now the radioactive methods of detecting and measuring B
are many milhons of miUions of times more dehcate than
the chemical methods of detecting and measuring A, so that
by mixing with A a small quantity of B we can trace its presence
far beyond the limits of chemical analysis. We have, as it
were, marked the atoms of A with an indelible label so that
the minutest trace of the element can be measured with ease
and certainty.
By this powerful and novel device, which has been developed
by G. Hevesy ^ 10~^ gr. of lead can be determined quantitatively and solution concentrations can be dealt with down to
10"^* of normal. By adding radium D to the lead salt and
estimating it electroscopically the solubihty of lead sulphide
and chromate, and the amount of lead chloride carried down
in a silver chloride precipitate, may readily be determined.
Recently, by the same principle, it has been shown that a
free exchange of the metallic atom among the competing acid
radicles occurs for ionised, but not for non-ionised, compounds.
The general method was to mix solutions of two different
compounds of lead in equimolecular proportions, the one
compound only being " activated " by presence of thorium-B
(which is isotopic with lead), and to determine the activity of
the lead in the less soluble compound crystalHsing out. When
active lead nitrate and inactive lead chloride are dissolved
in molecular proportion in boiling pyridine, the lead in the
lead chloride crystalHsing out is half as active as the lead in
the original lead nitrate, but when such an active lead salt
is so mixed with an organic compound of lead, such as lead
tetraphenyl or diphenyl nitrate, in suitable solvents, no inter
1 Hevesy, Brit. Assoc, 1913 ;  Chem. News, Oct. 13, 166,  1913.
change of lead occurs, and the active lead salt retains its
original activity. This constitutes something like a direct
proof of the ionic dissociation theory and of the current views
as to the difference between the nature of chemical union in
electrolytes and non-electrolytes. When the acetates of
quadrivalent activated lead and of bivalent inactive lead are
mixed in glacial acetic acid, the activity of the first compound,
after crystallising out from the mixture, is reduced to one
half. This indicates, since the two lead ions differ only by
two electrons, a free interchange of electrons between them
and a dynamic equilibrium between ions and electrons
and between free electrons and the electrodes in electrolysis. ^
Isotopes can also be used to determine the velocity of
diffusion of molecules among themselves.^ The rate of diffusion is dependent on the molecular diameter, and not on the
mass, so that a radioactive element diffusing among the
inactive molecules of its isotope affords a means of investigating this otherwise insoluble problem. The experiment has
been tried with molten lead. At the bottom of a narrow
vertical tube was placed a layer of lead rendered active by
the presence of thorium-B, and above it a layer three times
the height of common lead. The whole was kept at 340=C2=B0
for several days. After cooling, the cyhnder was cut into
four equal lengths, each melted and hammered into foil, and
the concentration of thorium-B in each determined by alpha
ray measurements. Values for the diffusion coefficient between
1-77 and 2-54 per sq. cm. per day, with a mean of 222 in
seventeen experiments, were obtained. On certain theories
of physical chemistry this corresponds with a diameter of the
lead molecule between 0-78 and IIQ x 10"^ cm., according to
the formulae used to connect the two quantities. The value
found by similar theories when reduced to a temperature of
18=C2=B0 and for a fluid of the viscosity of water, becomes 2-13.
Since the value for lead ions diffusing in aqueous solutions is
0-68, this indicates that the molecular diameter in the case
1 G. Hevesy and L. Zechmeister, Ber., 53B, 410, 1920 ; Zeitsch.
Elektrochem. 26, 151,  1920.
2 J. Groh and Hevesy, Ann. Physik., iv., 63, 85,  1920.
of metallic lead is only a third of that in the case of the ion, and shows that the latter is probably hydrated.^
===13. Classification of the radioactive isotopes===
It is
clear that the relations between isotopes formed by radioactive
disintegrations need not necessarily have the same simple form
as those subsisting between isotopes of the inactive elements.
Neubm'ger,^ using the nucleus model of the radioelements
proposed by Lise Meitner,^ suggests that the radioactive isotopes may be divided into three or even four classes.
(1) Isotopes of the first class are those which possess only
the same nuclear charge and the same arrangement of outer
electrons such as radium and mesothorium I.
(2) Isotopes of the second class have, in addition, the same
nuclear mass, that is to say the same atomic weight, and the
same total number of nuclear " building stones." Examples
of this class are ionium and uranium Y.
(3) Isotopes of the third class still possess the same number
of each nuclear building stone, but they have a different
arrangement of these in the atomic nucleus, and thus possess
different chances of disintegrating, such as Radium D and
Actinium B.
(4) Isotopes of the fourth class would be those possessing
the same arrangement of nuclear building stones in the atomic
nucleus, and thus the same probabihty of disintegrating.
Such isotopes actually exist, but we have no available means
of distinguishing between them. Hence we cannot at present
designate them definitely as isotopes. Examples of these are
radium Cg and actinium D.
^ Soddy, Ann. Rep. Chem. Soc, 227,  1920.
2 Neuburger, Nature, 108, 180,  1921.
^ Meitner, Die Naturwissenschaften, 9, 423,  1921.
==References=<references/>er  in  any  proportions  no  chemical
or  physical  process  known  is  capable  of  altering  the  ratio  of
the  proportions  of  this  mixture  to  any  measurable  extent.
Now  the  radioactive  methods  of  detecting  and  measuring  B
are  many  milhons  of  miUions  of  times  more  dehcate  than
the  chemical  methods  of  detecting  and  measuring  A,  so  that
by  mixing  with  A  a  small  quantity  of  B  we  can  trace  its  presen=
ce
far  beyond  the  limits  of  chemical  analysis.  We  have,  as  it
were,  marked  the  atoms  of  A  with  an  indelible  label  so  that
the  minutest  trace  of  the  element  can  be  measured  with  ease
and  certainty.
By  this  powerful  and  novel  device,  which  has  been  developed
by  G.  Hevesy  ^  10~^  gr.  of  lead  can  be  determined  quantita-
tively and  solution  concentrations  can  be  dealt  with  down  to
10"^*  of  normal.  By  adding  radium  D  to  the  lead  salt  and
estimating  it  electroscopically  the  solubihty  of  lead  sulphide
and  chromate,  and  the  amount  of  lead  chloride  carried  down
in  a  silver  chloride  precipitate,  may  readily  be  determined.
Recently,  by  the  same  principle,  it  has  been  shown  that  a
free  exchange  of  the  metallic  atom  among  the  competing  acid
radicles  occurs  for  ionised,  but  not  for  non-ionised,  compounds.
The  general  method  was  to  mix  solutions  of  two  different
compounds  of  lead  in  equimolecular  proportions,  the  one
compound  only  being  "  activated  "  by  presence  of  thorium-B
(which  is  isotopic  with  lead),  and  to  determine  the  activity  of=
the  lead  in  the  less  soluble  compound  crystalHsing  out.  When
active  lead  nitrate  and  inactive  lead  chloride  are  dissolved
in  molecular  proportion  in  boiling  pyridine,  the  lead  in  the
lead  chloride  crystalHsing  out  is  half  as  active  as  the  lead  in=
the  original  lead  nitrate,  but  when  such  an  active  lead  salt
is  so  mixed  with  an  organic  compound  of  lead,  such  as  lead
tetraphenyl  or  diphenyl  nitrate,  in  suitable  solvents,  no  inter-
1  Hevesy,  Brit.  Assoc,  1913  ;  Chem.  News,  Oct.  13,  166,    1913=
.
change  of  lead  occurs,  and  the  active  lead  salt  retains  its
original  activity.  This  constitutes  something  like  a  direct
proof  of  the  ionic  dissociation  theory  and  of  the  current  views
as  to  the  difference  between  the  nature  of  chemical  union  in
electrolytes  and  non-electrolytes.  When  the  acetates  of
quadrivalent  activated  lead  and  of  bivalent  inactive  lead  are
mixed  in  glacial  acetic  acid,  the  activity  of  the  first  compound,
after  crystallising  out  from  the  mixture,  is  reduced  to  one
half.  This  indicates,  since  the  two  lead  ions  differ  only  by
two  electrons,  a  free  interchange  of  electrons  between  them
and  a  dynamic  equilibrium  between  ions  and  electrons
and  between  free  electrons  and  the  electrodes  in  electro-
lysis. ^
Isotopes  can  also  be  used  to  determine  the  velocity  of
diffusion  of  molecules  among  themselves.^  The  rate  of  diffu-
sion is  dependent  on  the  molecular  diameter,  and  not  on  the
mass,  so  that  a  radioactive  element  diffusing  among  the
inactive  molecules  of  its  isotope  affords  a  means  of  investi-
gating this  otherwise  insoluble  problem.  The  experiment  has
been  tried  with  molten  lead.  At  the  bottom  of  a  narrow
vertical  tube  was  placed  a  layer  of  lead  rendered  active  by
the  presence  of  thorium-B,  and  above  it  a  layer  three  times
the  height  of  common  lead.  The  whole  was  kept  at  340=C2=B0
for  several  days.  After  cooling,  the  cyhnder  was  cut  into
four  equal  lengths,  each  melted  and  hammered  into  foil,  and
the  concentration  of  thorium-B  in  each  determined  by  alpha
ray  measurements.  Values  for  the  diffusion  coefficient  between
1-77  and  2-54  per  sq.  cm.  per  day,  with  a  mean  of  222  in
seventeen  experiments,  were  obtained.  On  certain  theories
of  physical  chemistry  this  corresponds  with  a  diameter  of  the
lead  molecule  between  0-78  and  IIQ  x  10"^  cm.,  according  to
the  formulae  used  to  connect  the  two  quantities.  The  value
found  by  similar  theories  when  reduced  to  a  temperature  of
18=C2=B0  and  for  a  fluid  of  the  viscosity  of  water,  becomes  2-13=
.
Since  the  value  for  lead  ions  diffusing  in  aqueous  solutions  is=
0-68,  this  indicates  that  the  molecular  diameter  in  the  case
1 G.  Hevesy  and  L.  Zechmeister,  Ber.,  53B,  410,  1920 ;  Zeitsch.
Elektrochem.  26,  151,    1920.
2  J.  Groh  and  Hevesy,  Ann.  Physik.,  iv.,  63,  85,    1920.
of  metallic  lead  is  only  a  third  of  that  in  the  case  of  the  i=
on, and  shows  that  the  latter  is  probably  hydrated.^
==References==
<references/>
<references/>


===13.  Classification  of  the  radioactive  isotopes=== 
----
It  is
clear  that  the  relations  between  isotopes  formed  by  radioactive
disintegrations  need  not  necessarily  have  the  same  simple  form
as  those  subsisting  between  isotopes  of  the  inactive  elements.
Neubm'ger,^  using  the  nucleus  model  of  the  radioelements
proposed  by  Lise  Meitner,^  suggests  that  the  radioactive  iso-
topes may  be  divided  into  three  or  even  four  classes.
 
(1)  Isotopes  of  the  first  class  are  those  which  possess  only
the  same  nuclear  charge  and  the  same  arrangement  of  outer
electrons  such  as  radium  and  mesothorium  I.
 
(2)  Isotopes  of  the  second  class  have,  in  addition,  the  same
nuclear  mass,  that  is  to  say  the  same  atomic  weight,  and  the
same  total  number  of  nuclear  "  building  stones."  Examples
of  this  class  are  ionium  and  uranium  Y.
 
(3)  Isotopes  of  the  third  class  still  possess  the  same  number
of  each  nuclear  building  stone,  but  they  have  a  different
arrangement  of  these  in  the  atomic  nucleus,  and  thus  possess
different  chances  of  disintegrating,  such  as  Radium  D  and
Actinium  B.
 
(4)  Isotopes  of  the  fourth  class  would  be  those  possessing
the  same  arrangement  of  nuclear  building  stones  in  the  atomic
nucleus,  and  thus  the  same  probabihty  of  disintegrating.
Such  isotopes  actually  exist,  but  we  have  no  available  means
of  distinguishing  between  them.  Hence  we  cannot  at  present
designate  them  definitely  as  isotopes.  Examples  of  these  are
radium  Cg  and  actinium  D.
 
^  Soddy,  Ann.  Rep.  Chem.  Soc,  227,    1920.
 
2  Neuburger,  Nature,  108,  180,    1921.


^  Meitner,  Die  Naturwissenschaften,  9,  423,    1921.
{{Template:Aston 1922 Contents}}

Latest revision as of 15:02, 31 July 2025

Chapter II - The Radioactive Isotopes

Francis William Aston (1922), Isotopes, ISBN 978-1016732383, Internet Archive.

5. Chemical identities among the radioactive elements

Apart from the purely speculative considerations which have aheady been detailed, the theory of isotopes had its birth in the gigantic forward wave of human knowledge inaugurated by the discovery of radioactivity. It can admittedly be argued that, even if no radioactive elements existed, isotopes would inevitably have been discovered by the method of positive rays. But progress must then have been exceedingly slow, and the arrival at the real interpretation of the idea, depending as it does on Sir Ernest Rutherford's theory of the " nucleus" atom, almost impossible.

In 1906 Boltwood at Yale discovered a new element in the radioactive group which he called Ionium,[1] and described as having chemical properties similar to those of thorium. So much was this the case that if, by accident, salts of these two elements were mixed, he found it impossible to separate them again by any of the chemical processes.

Boltwood, being occupied in the experimental proof that ionium was the parent substance of radium, did not pursue this line of investigation further at the time, but the work was later taken in hand by Marckwald and Keetman of Berlin.[2] Thanks to the rapid advance in radioactive methods there were now at command means of detecting change in concentration of a delicacy unheard of in the previous work on the rare earths, but yet, after years of patient and laborious work, not the slightest sign of separation of ionium and thorium could be observed. The chemical similarity between these two bodies was therefore of an order entirely different to that exhibited by the rare earth elements, and came as near absolute identity as the most critical mind could require.

This result was confirmed in the most rigorous manner by Auer v. Welsbach[3] who was able to apply to the problem his valuable experience in work on the rare earths.

Furthermore, Mesothorium, discovered by Hahn in 1907, was shown to be chemically inseparable from radium by Marckwald[4] and Soddy[5] and similar chemical identities were shown to be exceedingly probable in many other cases of radioactive products. Certain regularities in the occurrence of these were pointed out by Hahn and Meitner.[6]

The situation was admirably summed up by Soddy in his report on radioactivity for the year 1910[7] in the following words:

"These regularities may prove to be the beginning of some embracing generalisation, which will throw light, not only on radioactive processes, but on elements in general and the Periodic Law. Of course, the evidence of chemical identity is not of equal weight for all the preceding cases, but the complete identity of ionium, thorium and radiothorium, of radium and mesothorium 1, of lead and radium D, may be considered thoroughly established. . . . The recognition that elements of different atomic weights may possess identical properties seems destined to have its most important apphcation in the region of inactive elements, where the absence of a second radioactive nature makes it impossible for chemical identity to be individually detected. Chemical homogeneity is no longer a guarantee that any supposed element is not a mixture of several of different atomic weights, or that any atomic weight is not merely a mean number. The constancy of atomic weight, whatever the source of the material, is not a complete proof of homogeneity, for, as in the radioelements, genetic relationships might have resulted in an initial constancy of proportion between the several individuals, which no subsequent natural or artificial chemical process would be able to disturb. If this is the case, the absence of simple numerical relationships between the atomic weights becomes a matter of course rather than one of surprise."

6. Spectroscopic identity of isotopes

The next great advance was of an even more revolutionary character. This consisted in the demonstration that the chemically indistinguishable products of the transformation of the radioactive elements might also be spectroscopically identical. The idea that elements of different atomic weight might yet have the same spectrum originated in Sir Ernest Rutherford's laboratory and appears to have been first entertained by A. S. Russell. With Rossi[8] he undertook the comparison between the spectrum of pure thorium and that of a mixture of thorium and ionium which radioactive evidence showed to contain a large percentage of the latter element. No new fines attributable to ionium were observed; in fact the spectra obtained were absolutely indistinguishable.

After giving in full the radioactive evidence as to the probable percentage of ionium present, and showing that it was practically impossible for this to be too small for its spectrum to appear, the writers go on as follows:

"There are, however, two other possible ways of explaining our failure to obtain a distinct spectrum for ionium, besides the one discussed above. It is possible that :

"(1) Ionium has no arc spectrum in the region investigated,

or

"(2) Ionium and thorium have identical spectra in the region investigated.

"The first possibility is highly improbable, for all solids of high atomic weights have arc spectra, and, further, aU rare earths have highly complicated spectra.

"The second possibility, though somewhat speculative in nature, is suggested by some recent work on the chemical properties of the radio-elements. There is no evidence at present to disprove its truth. It is well known that there are no less than four sets of longlived radio-elements, the members of each of which are chemically non-separable. These elements do not all belong to the group of rare earths, many non-radioactive members of which are known to be chemically very similar. Mesothorium, for instance, which is chemically non-separable ' from radium, belongs to the alkaline earth group. Again the two non-separable a ray products which are present in ordinary uranium, and which have been called by Geiger and Nuttall uranium I and uranium II belong to the chromium-molybdenum-tungsten group of elements. The explanation of these striking chemical similarities is very probably that the two very similar bodies are really different members of the same group of elements, the difference in their chemical properties being less pronounced than the difference between other members of the same group, owing to the small difference in their atomic weights. But the possibility that they are identical in all physical and chemical properties, and differ only in atomic weight and in radioactive properties, should not be lost sight of. If this explanation should eventually prove justified, the spectrum of ionium would he identical with that of thorium."

It is not surprising that the idea was put forward with some caution. Unlike that of chemical identity which had been led up to by a gradual series of steps, it was entirely new and contrary to all the preconceived ideas of the relations between the spectrum of an element and the masses of its atoms. The new departure was supported by Soddy[9] but received some adverse criticism on the ground of insufficient evidence. The later work bearing on this point will be described in Chapter X.

Already in 1911 the theory of the "Nucleus Atom"[10] had been formulated. This gave the first hint as to the physical meaning of chemical and spectroscopic identity, namely that the nuclei of atoms might vary in their mass but yet, at the same time, possess some property in common with each other, namely nuclear charge, upon which the chemistry and spectra depend.

In 1912 appeared the electrochemical work of Hevesy,[11] which led to the discovery of the remarkable field of research opened up by the use of radioactive bodies as indicators.[12] A little later Paneth and Hevesy were able to show the complete identity of the electrochemical properties of Radium D and Lead.[13]

In 1914 Rutherford and Andrade[14] examined the self-excited X-ray spectrum of radium B. They used a crystal of rock salt for the analysis and got rid of the effect of the swift β rays by putting the source in a strong magnetic field. The wave length of the L radiation proved to be exactly that expected for lead from Moseley's experiment.[15] This was the first proof that isotopes had identical X-ray spectra. The actual values for ordinary lead were subsequently determined by [[wikipedia:Manne Siegbahn|Siegbahn and found to be in excellent agreement with Rutherford and Andrade's results.

7. The Chemical Law of Radioactive change

This law, put in the briefest form, asserts: A radioactive element when it loses an alpha particle goes back two places in the Periodic Table; when it loses a beta particle it goes forward one place.

The law has been associated with the name of Soddy[16] who was the first to suggest, in the form of a valency property, that part of it relating to alpha rays.[17] But in its more complete enunciation, which took place early in 1913, at least four other investigators can claim a share.

Russell was the first to publish a law covering both Kinds of rays,[18] but owing to the fact that he failed to realise that the sequence of elements in the periodic table is a continuous expression, his statement was not so simple and definite as it might have been. Fajans,[19] using as foundation the electrochemical results of Hevesy,[20] and Soddy, working on the results of a very full chemical investigation carried out at his request by Fleck,[21] published the generalisation in its full and complete form independently, and practically at the same time.

This law, which will be shown later to be a natural consequence of the much wider generalisation discovered by Moseley,[22] has been of the greatest value in correlating the numerous products of radioactive change, and predicting with accuracy which of them mil have identical properties. To the latter the name Isotopes was appled by Soddy in the following words: "The same algebraic sum of the positive and negative charges in the nucleus when the arithmetical sum is different gives what I call 'isotopes' or 'isotopic elements' because they occupy the same place in the periodic table. They are chemically identical, and save only as regards the relatively few physical properties which depend upon atomic mass directly, physically identical also." Any element which is the result of a series of changes involving the loss of twice as many beta particles as alpha particles must clearly be the isotope of the parent element, since it must inevitably, by the above law, reach the same place in the periodic table at the end of these operations.

8. Isobares

Just as we can have elements of the same chemical properties but different atomic weight so we can also have those with the same atomic weight but different chemical properties. These Stewart [23] has called "Isobares." Any product due to the loss of a beta ray (which has a negligible mass)[24] must be an isobare of its parent substance, for, without change of mass, it has moved in the periodic table and so changed its chemical properties. It is interesting to note in this connection that no isobare has actually been discovered among the non-radioactive elements as yet, but they must certainly exist.[25]

9. The Radioactive Transformations

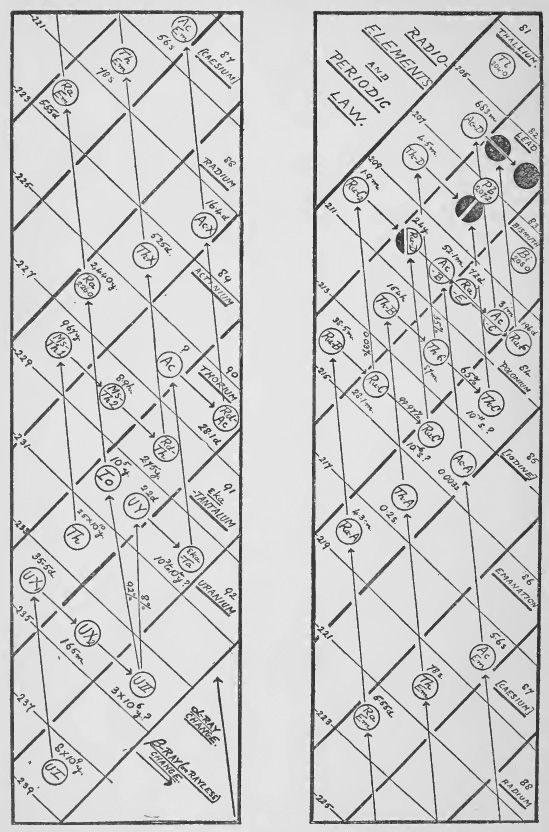
Fig. 1. Diagram of the transformations of the radio-elements showing atomic number, atomic weight and period of disintegration of each product.

The radioactive elements are all formed from the two parent elements inanium and thorium by a series of changes or transformations. These changes can be classified according to their nature into two types. In the first type of change called the α ray change the atom loses a particle of mass 4 carrying two positive charges {+2e) which has been identified with the nucleus of the helium atom.^[26] In the second or β ray change the particle shot off has a negligible mass and carries a single negative charge (–e). Hence in an a ray change the element loses 4 units in atomic weight, while in a β ray change its weight is unaltered.

The rate of decay of an element is measured by the " half value " period which may vary from 1010 years to 10-11 of a second. The velocity with which the rays are ejected also varies and is apparently connected with the period of the element by the very interesting relation of [[wikipedia:Geiger–Nuttall law|Geiger and Nuttall.[27] The intricate researches by which the complex series of transformations have been explained belong to the subject of Radioactivity and cannot be described here. From the point of view of isotopes it will be enough to consider the final results which are given in the two diagrams (Figs. 1 and 2).

In the first of these, which is due to Soddy,[28] the nuclear charge or Atomic number,[29] upon which all the chemical and spectroscopic properties of the elements depend, and which expresses its position in the periodic table, is indicated by a series of columns edged with thick fines sloping downwards to the right. The atomic weights are shown by fine lines sloping in the opposite direction. The fines corresponding to even atomic weights have been omitted to simplify the scheme. All elements lying in the same column will therefore be isotopes and all elements lying on the same fine sloping up to the right will be isobares. The α and β ray changes are shown by arrows and the period of decay of the elements indicated by times expressed in suitable units.

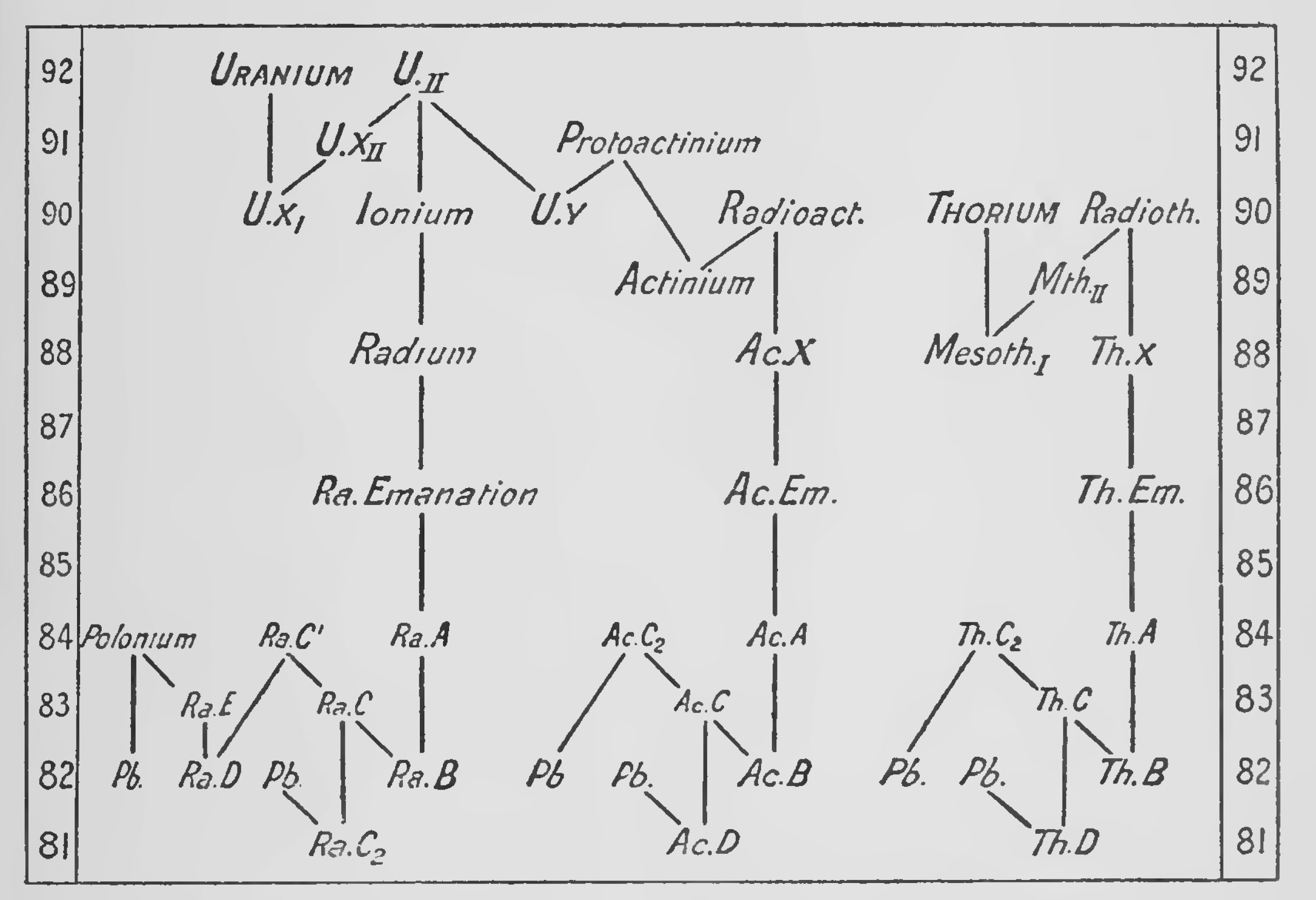
Fig. 2. Diagram of the radioactive transformations in relation to atomic numbers. In every case a step two downwards is accompanied by the emission of an a particle and one downwards by a β particle.

The second diagram[30] is arranged in a simple manner to show the general chains of transformation at a glance. In it the α and βray changes are plotted against atomic number and the other information omitted. On this diagram all elements lying on the same horizontal level will be isotopes. To take an example, uranium I which has an atomic number 92 and an atomic weight 238 loses one α particle and becomes uranium X, atomic number 90, atomic weight 234, This then gives off two β rays in succession, first becoming uranium X2 and then Uranium II. Uranium II has an atomic number 92 so that it is an isotope of uranium I. It has an atomic weight 234 so it is anisobare of uranium Xi and uranium X2. Uranium II can disintegrate by shooting off an a particle in two different ways ; about 8 per cent, of its atoms appear to form uranium Y, which is probably the parent substance of the actinium series. Disregarding this for the moment and following the main chain, 92 per cent, of the atoms of uranium II suffer an α ray change and are transformed into ionium, atomic weight 230, atomic number 90. Ionium loses an a particle and becomes radium, atomic weight 226. This by the same process changes to radium emanation, then to radium A, and then to radium B with atomic weight 214, We see that uranium II has lost 5 α particles in succession, thereby coming back 10 places, 92-82 in the periodic table, and its atomic weight has been reduced 20 units in the process. Radium B loses a β particle, becoming radium C which can disintegrate in two different ways. An extremely small proportion, 0.03 per cent., of its atoms undergo an α ray change to radium C2 which then loses a β particle and may become inactive lead of atomic weight 210. The vast majority of the atoms of radium C lose a β particle and form radium C. This next loses an a particle and becomes radium D, an active isotope of lead of atomic weight 210. Radium D now loses two β particles in succession, becoming radium E and then radium E, which is also called polonium. This finally undergoes its last a ray change and becomes inactive uranium lead of atomic weight 206.

The thorium and actinium chains can be followed on the diagrams in the same manner, but in the case of actinium the parent elements are not satisfactorily settled so that the atomic weights in this series are all doubtful.

10. The Atomic Weight of Lead

The theory of Isotopes of which Professor Soddy had proved himself so prominent an advocate and defender, received its most triumphant vindication, as far as it concerned the products of radioactivity, at the hands of the very chemists who had most reason to doubt its general apphcation, the specialists in the determination of atomic weights.

The charts of radioactive disintegration[31] show that the final product of every series is lead. If we take the main chain of the uranium-radium transformation this lead must have an atomic weight 206, for it has lost 5 alpha particles – each of weight 4 – since it was radium, and the atomic weight of radium is 226. On the other hand if we take the main thorium chain the lead end product must be 6 alpha particles lighter than thorium (232.15) and so should have an atomic weight about 208.

Now ordinary lead, from non-radioactive sources has an atomic weight 207.20, so Soddy[32] suggested in 1913 that the lead derived from minerals containing uranium but no thorium might have a smaller atomic weight than ordinary lead, and on the other hand the atomic weight of lead from minerals containing thorium but no uranium might be greater.

The first experiments were made by Soddy and Hyman[33] with a very small quantity of lead from Ceylon Thorite. This gave a perceptibly higher atomic weight than ordinary lead. Later a large quantity of the same mineral was available. The lead from this when carefully purified gave a density 0'26 per cent, higher than that of common lead. On the assumption that the atomic volumes of isotopes are equal this figure corresponds to an atomic weight of 207.74. A chemical atomic weight determination gave 207-694. A sample of the same lead was sent to Vienna where Professor Honigschmid, a well known expert in such matters, obtained from it a value 207.77 as a mean of eight determinations. These figures not only showed that thorium lead had a higher atomic weight than ordinary lead but also that their atomic volumes were identical, as expected from theory.[34]

At the same time as this work was in progress, the leading American authority on atomic weights, T. W. Richards of Harvard, started a series of investigations on lead derived from various radioactive minerals.[35] The samples of lead from uranium minerals all gave results lower than ordinary lead, as was expected, and one particularly pure specimen of uraniolead from Norwegian cleveite gave 206.08,[36] a very striking agreement with theory. The following table of properties is taken from his Presidential address to the American Association at Baltimore, December, 1918.


Common Lead Mixture Australian Uranio-Lead Percentage Difference
A B C A--B A--C
Atomic weight 207.19 206.34 206.08 0.42 0.54
Density 11.337 11.280 11.273 0.42 0.56
Atomic volume 18.277 18.278 18.281 0.01 0.02
Melting point (absolute) 600.53 600.59 --- 0.01 ---
Solubility (of nitrate) 37.281 37.130 --- 0.41 ---
Refractive Index (nitrate) 1.7815 1.7814 --- 0.01 ---
Thermoelectric effect --- --- --- 0.00 ---
Spectrum wave-length --- --- --- 0.00 0.00

In further confirmation Maurice Curie in Paris[37] reported 206.36 for a lead from carnotite, and a still lower figure, 206.046, was obtained by Honigschmid in Vienna for a lead from the very pure crystalised pitchblende from Morogoro. This is the lowest atomic weight found so far. The highest, 207.9, was also determined by Honigschmid for lead from Norwegian thorite.[38]

11. Atomic weights of Thorium and Ionium

Although the above results obtained with lead are far the most conclusive and important it is not the only element which affords direct experimental evidence of the different atomic weights of isotopes. The atomic weight of ionium, calculated by adding the weight of one alpha particle to the atomic weight of its product, radium, is 230, whereas that of thorium, its isotope, is slightly above 232. Joachimsthal pitchblende contains hardly any thorium so that an ionium-thorium preparation separated by Auer von Welsbach from 30 tons of this mineral might be regarded as containing a maximum concentration of ionium. On the other hand the period of thorium is about 105 times longer than that of ionium so that it was doubtful if even in this preparation there would be enough ionium to show a difference in atomic weight. Honigschmid and Mlle. Horovitz have made a special examination of this point, first redetermining as accurately as possible the atomic weight of thorium and then that of the thorium-ionium preparation from pitchblende. They found 232.12 for the atomic weight of thorium, and by the same careful method 231.51 for that of the thorium-ionium.

12. Use of radioactive isotopes as indicators

Consider an inactive element A which has a radioactive isotope B. If these are mixed together in any proportions no chemical or physical process known is capable of altering the ratio of the proportions of this mixture to any measurable extent. Now the radioactive methods of detecting and measuring B are many millions of millions of times more delicate than the chemical methods of detecting and measuring A, so that by mixing with A a small quantity of B we can trace its presence far beyond the limits of chemical analysis. We have, as it were, marked the atoms of A with an indelible label so that the minutest trace of the element can be measured with ease and certainty.

By this powerful and novel device, which has been developed by G. Hevesy[39] 10-9 gr. of lead can be determined quantitatively and solution concentrations can be dealt with down to 10-14 of normal. By adding radium D to the lead salt and estimating it electroscopically the solubility of lead sulphide and chromate, and the amount of lead chloride carried down in a silver chloride precipitate, may readily be determined.

Recently, by the same principle, it has been shown that a free exchange of the metallic atom among the competing acid radicles occurs for ionised, but not for non-ionised, compounds. The general method was to mix solutions of two different compounds of lead in equimolecular proportions, the one compound only being "activated" by presence of thorium-B (which is isotopic with lead), and to determine the activity of the lead in the less soluble compound crystallising out. When active lead nitrate and inactive lead chloride are dissolved in molecular proportion in boiling pyridine, the lead in the lead chloride crystalHsing out is half as active as the lead in the original lead nitrate, but when such an active lead salt is so mixed with an organic compound of lead, such as lead tetraphenyl or diphenyl nitrate, in suitable solvents, no interchange of lead occurs, and the active lead salt retains its original activity. This constitutes something like a direct proof of the ionic dissociation theory and of the current views as to the difference between the nature of chemical union in electrolytes and non-electrolytes. When the acetates of quadrivalent activated lead and of bivalent inactive lead are mixed in glacial acetic acid, the activity of the first compound, after crystallising out from the mixture, is reduced to one half. This indicates, since the two lead ions differ only by two electrons, a free interchange of electrons between them and a dynamic equilibrium between ions and electrons and between free electrons and the electrodes in electrolysis.[40]

Isotopes can also be used to determine the velocity of diffusion of molecules among themselves.[41] The rate of diffusion is dependent on the molecular diameter, and not on the mass, so that a radioactive element diffusing among the inactive molecules of its isotope affords a means of investigating this otherwise insoluble problem. The experiment has been tried with molten lead. At the bottom of a narrow vertical tube was placed a layer of lead rendered active by the presence of thorium-B, and above it a layer three times the height of common lead. The whole was kept at 340° for several days. After cooling, the cylinder was cut into four equal lengths, each melted and hammered into foil, and the concentration of thorium-B in each determined by alpha ray measurements. Values for the diffusion coefficient between 1.77 and 2.54 per sq. cm. per day, with a mean of 222 in seventeen experiments, were obtained. On certain theories of physical chemistry this corresponds with a diameter of the lead molecule between 0.78 and I1.16 x 10-8 cm., according to the formulae used to connect the two quantities. The value found by similar theories when reduced to a temperature of 18° and for a fluid of the viscosity of water, becomes 2.13. Since the value for lead ions diffusing in aqueous solutions is 0.68, this indicates that the molecular diameter in the case of metallic lead is only a third of that in the case of the ion, and shows that the latter is probably hydrated.[42]

13. Classification of the radioactive isotopes

It is clear that the relations between isotopes formed by radioactive disintegrations need not necessarily have the same simple form as those subsisting between isotopes of the inactive elements. Neuberger,[43] using the nucleus model of the radioelements proposed by Lise Meitner,[44] suggests that the radioactive isotopes may be divided into three or even four classes.

(1) Isotopes of the first class are those which possess only the same nuclear charge and the same arrangement of outer electrons such as radium and mesothorium I.
(2) Isotopes of the second class have, in addition, the same nuclear mass, that is to say the same atomic weight, and the same total number of nuclear "building stones." Examples of this class are ionium and uranium Y.
(3) Isotopes of the third class still possess the same number of each nuclear building stone, but they have a different arrangement of these in the atomic nucleus, and thus possess different chances of disintegrating, such as Radium D and Actinium B.
(4) Isotopes of the fourth class would be those possessing the same arrangement of nuclear building stones in the atomic nucleus, and thus the same probability of disintegrating. Such isotopes actually exist, but we have no available means of distinguishing between them. Hence we cannot at present designate them definitely as isotopes. Examples of these are radium C2 and actinium D.

References

  1. ↑ Boltwood, Amer. J. Sci, 22, 537, 1906;[1] 24, 370, 1907.[2]
  2. ↑ Keetman, Jahr. Radioactivitat, 6, 269, 1909.
  3. ↑ A. von Welsbach, Wien. Ber. iia, 119, 1011, 1910.
  4. ↑ Marckwald, Ber. d. Chem. Oes., 40, 3420, 1910.
  5. ↑ Soddy, Trans. Chem. Soc, 99, 72, 1911.
  6. ↑ Hahn and Meitner, Physikal. Zeitsch., 11, 493, 1910.
  7. ↑ Soddy, Chem. Soc. Ann. Rep., 285, 1910.
  8. ↑ Russell and Rossi, Proc. Roy. Soc, 77A, 478, 1912.
  9. ↑ Soddy, Chem. News, Feb. 28, 1913.
  10. ↑ V. p. 92.
  11. ↑ G. Hevesy, Phil. Mag., 23, 628, 1912 ; Physikal. Zeitsch. 15, 672, 715, 1912.
  12. ↑ V. p. 19.
  13. ↑ Paneth and Hevesy, Sitzungber. K. Akad. Wiss. Wien, iiA, 123, 1037, 1913.
  14. ↑ Rutherford and Andrade, Phil. Mag. 27, 854, 1914.
  15. ↑ V. p. 93.
  16. ↑ V. Stewart, Recent Advances in Physical and Inorganic Chemistry, Longmans, 1919.
  17. ↑ Soddy, The Chemistry of the Radio Elements, 29, First Edition, Longmans, 1911.
  18. ↑ Russell, Chem. News, Jan, 31, 1913,
  19. ↑ Fajans, Physikal. Zeitsch. Feb. 15, 1913.
  20. ↑ Hevesy, Physikal. Zeitsch. Jan. 15, 1913.
  21. ↑ Fleck, Trans. Chem. Soc. 103, 381, 1052, 1913.
  22. ↑ V. p. 93.
  23. ↑ Stewart, Phil. Mag. 36, 326, 1918.[3]
  24. ↑ V. p. 91.
  25. ↑ V. p. 77.
  26. ↑ V. Table p. 106.
  27. ↑ Rutherford, Radioactive Substances and their Radiations, p. 607, Cambridge, 1913.
  28. ↑ Soddy, Trans. Chem. Soc, U5, 16, 1919.
  29. ↑ V. p. 93.
  30. ↑ Darwin, Nature, 106, 82, 1920.[4]
  31. ↑ P. 14.
  32. ↑ 1 Soddy, Ann. Rep. Chem. Soc, 269, 1913.
  33. ↑ 2 Soddy and Hyman, Trans. Chem. Soc, 105, 1402, 1914.
  34. ↑ Soddy, Roy. Ins., May 18, 1917.
  35. ↑ Richards and Lembert, J. Amer. Chem. Soc, 36, 1329, 1914. [5]
  36. ↑ 5 Richards and Wadsworth, J. Amer. Chem. Soc, 38, 2613, 1916.
  37. ↑ M. Curie, Compt. Bend., 158, 1676, 1914.
  38. ↑ Honigschmid, Zeit. Elektrochem., 24, 163, 1918 ; 25, 91, 1919.
  39. ↑ Hevesy, Brit. Assoc, 1913 ; Chem. News, Oct. 13, 166, 1913.
  40. ↑ G. Hevesy and L. Zechmeister, Ber., 53B, 410, 1920 ; Zeitsch. Elektrochem. 26, 151, 1920.
  41. ↑ J. Groh and Hevesy, Ann. Physik., iv., 63, 85, 1920.
  42. ↑ Soddy, Ann. Rep. Chem. Soc, 227, 1920.
  43. ↑ Neuburger, Nature, 108, 180, 1921.
  44. ↑ Meitner, Die Naturwissenschaften, 9, 423, 1921.

Francis William Aston (1922), Isotopes, ISBN 978-1016732383, Internet Archive.

Retrieved from "https://msterms.org/wiki/index.php?title=Aston_1922/Chapter_2&oldid=21771"